题目内容
在正三棱柱ABC-A1B1C1中,若AB=2,AA1=1,则点A到平面A1BC的距离为( )
A.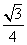 B.
B.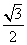 C.
C.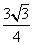 D.
D.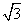
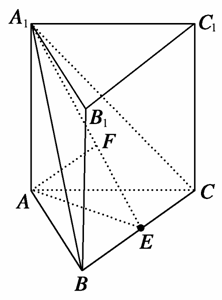
B
[解析] 解法1:取BC中点E,连接AE、A1E,过点A作AF⊥A1E,垂足为F.
∵A1A⊥平面ABC,∴A1A⊥BC,
∵AB=AC.∴AE⊥BC.
∴BC⊥平面AEA1.
∴BC⊥AF,又AF⊥A1E,
∴AF⊥平面A1BC.
∴AF的长即为所求点面距离.
AA1=1,AE=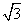 ,∴AF=
,∴AF=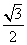 .
.
解法2:VA1-ABC=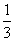 S△ABC·AA1=
S△ABC·AA1=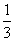 ×
×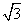 ×1=
×1=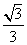 .
.
又∵A1B=A1C=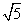 ,
,
在△A1BE中,A1E=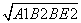 =2.
=2.
∴S△A1BC=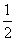 ×2×2=2.
×2×2=2.
∴VA-A1BC=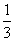 ×S△A1BC·h=
×S△A1BC·h=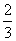 h.
h.
∴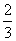 h=
h=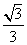 ,∴h=
,∴h=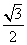 .
.
∴点A到平面A1BC距离为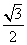 .
.
解法3:设BC中点为O,∵△ABC为正三角形,
∴AO⊥BC,
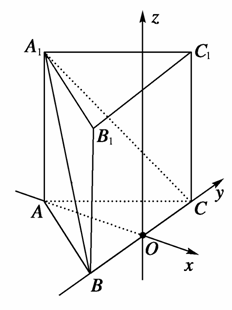
以O为原点,直线AO,BC分别为x轴、y轴建立如图所示空间直角坐标系,则B(0,-1,0),C(0,1,0),A(-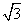 ,0,0),A1(-
,0,0),A1(- ,0,1).
,0,1).
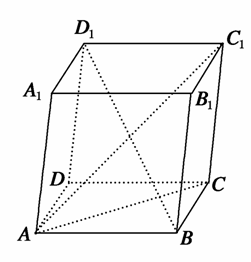
设n=(x,y,1)为平面A1BC的一个法向量,则


练习册系列答案
相关题目
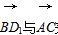 夹角的余弦值.
夹角的余弦值.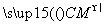 ,
,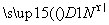 >的值为( )
>的值为( )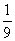 B.
B.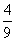
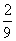
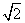
 的焦点与双曲线
的焦点与双曲线 的焦点重合,则
的焦点重合,则 的值为 .
的值为 .