题目内容
10.已知直线l1:ax+(a+2)y+2=0和l2:x+ay+1=0,若l1∥l2则a=-1.分析 由a•a-(a+2)=0,解得a,检验此时两条直线是否重合即可得出.
解答 解:由a•a-(a+2)=0,解得a=-1或2,
经过检验a=2时两条直线重合,舍去.
因此l1∥l2,则a=-1.
故答案为:-1.
点评 本题考查了平行线的充要条件、方程的解法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
1.已知一个圆锥的正视图和侧视图都是边长为1的正三角形,则它的俯视图的面积是( )
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
18.一个棱长为6的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体棱长的最大值为( )
| A. | 3 | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
2.执行如图所示的程序框图,则输出的a值为( )
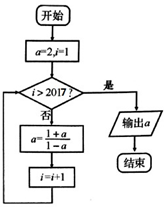

| A. | -3 | B. | $\frac{1}{3}$ | C. | $-\frac{1}{2}$ | D. | 2 |
19.以(1,0),(-1,0)为焦点的椭圆与y=x-2有公共点,则该椭圆离心率的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
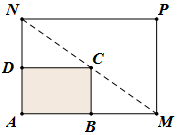 如图所示,某小区内有一矩形花坛,现将这一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.
如图所示,某小区内有一矩形花坛,现将这一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.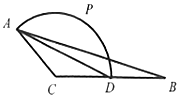 已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中点.
已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中点.