题目内容
20.设动点P(x,y)(x≥0)到定点F(1,0)的距离比它到y轴的距离大1,记点P的轨迹为曲线C.(Ⅰ)求曲线C的方程;
(Ⅱ)设D(x0,2)是曲线C上一点,与两坐标轴都不平行的直线l1,l2过点D,且它们的倾斜角互补.若直线l1,l2与曲线C的另一交点分别是M,N,证明直线MN的斜率为定值.
分析 (Ⅰ)由题意知,动点P(x,y)(x≥0)到定点F(1,0)的距离等于点P(x,y)到直线x=-1的距离,由抛物线的定义知点P的轨迹方程.
(Ⅱ)由D(x0,2)在曲线C上,得4=4x0⇒x0=1,从而D(1,2),设而不求的思想,利用韦达定理,通过直线l1,l2过点D,且它们的倾斜角互补建立关系,证明直线MN的斜率为定值.
解答 解:(Ⅰ)由题意知,动点P(x,y)(x≥0)到定点F(1,0)的距离等于点P(x,y)到直线x=-1的距离,
由抛物线的定义知点P的轨迹方程是以F(1,0)为焦点,以x=-1为准线的抛物线,
故曲线C的方程为y2=4x.
(Ⅱ)由D(x0,2)在曲线C上,得4=4x0⇒x0=1,从而D(1,2)
设M(x1,y1),N(x2,y2),
直线l1:y=k(x-1)+2,
则l2:y=-k(x-1)+2,
由$\left\{{\begin{array}{l}{y=k(x-1)+2}\\{{y^2}=4x}\end{array}}\right.⇒{k^2}{x^2}-(2{k^2}-4k+4)x+{(k-2)^2}=0$,
∴${x_1}×1=\frac{{{{(k-2)}^2}}}{k^2}=\frac{{{k^2}-4k+4}}{k^2}$
同理${x_2}=\frac{{{k^2}+4k+4}}{k^2}$,
∴${x_1}+{x_2}=\frac{{2{k^2}+8}}{k^2},{x_1}-{x_2}=\frac{-8}{k}$,
∴${y_1}-{y_2}=k({x_1}+{x_2})-2k=\frac{8}{k}$
∴${k_{MN}}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{{\frac{8}{k}}}{{-\frac{8}{k}}}=-1$
直线MN的斜率为定值-1.
点评 本题考查了抛物线的定义和直线与抛物线的位置关系的运用能力和计算能力.属于中档题.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
| A. | “sinα=$\frac{3}{5}$”是“cos2α=$\frac{7}{25}$”的必要不充分条件 | |
| B. | 已知命题p:?x∈R,使2x>3x;命题q:?x∈(0,+∞),都有$\frac{1}{{x}^{2}}$<$\frac{1}{{x}^{3}}$,则p∧(¬q)是真命题 | |
| C. | 命题“若xy=0,则x=0或y=0”的否命题是“若xy≠0,则x≠0或y≠0” | |
| D. | 从匀速传递的生产流水线上,质检员每隔5分钟从中抽取一件产品进行某项指标检测,这是分成抽样 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 一个几何体的三视图如图所示,图中矩形均为边长是1的正方形弧线为四分之一圆,则该几何体的体积是$1-\frac{π}{6}$.
一个几何体的三视图如图所示,图中矩形均为边长是1的正方形弧线为四分之一圆,则该几何体的体积是$1-\frac{π}{6}$.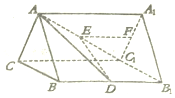 在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C为矩形,D,E,F分别是线段BB1,AC1,A1C1的中点.
在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C为矩形,D,E,F分别是线段BB1,AC1,A1C1的中点.