题目内容
19.以(1,0),(-1,0)为焦点的椭圆与y=x-2有公共点,则该椭圆离心率的最大值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
分析 设出椭圆的方程,求出离心率的平方,将直线方程代入椭圆方程得得到的关于x的一元二次方程的判别式大于0,求出 b2 的最小值,此时的离心率最大,求解即可.
解答 解:由题意知,c=1,a2-b2=1,故可设椭圆的方程为:$\frac{{x}^{2}}{{b}^{2}+1}+\frac{{y}^{2}}{{b}^{2}}=1$,
离心率的平方为 $\frac{1}{{b}^{2}+1}$ ①,∵直线x-y-2=0与椭圆有公共点,将直线方程代入椭圆方程得
(2b2+1)x2-4(b2+1)x+3b2+4-b4=0,由△=16(b4+2b2+1)-4(2b2+1)(3b2+4-b4)≥0,
∴2b4-3b2≥0,∴b2≥$\frac{3}{2}$,或 b2≤0(舍去),∴b2 的最小值为$\frac{3}{2}$,a2=$\frac{5}{2}$,
∴离心率最大值为:$\frac{\sqrt{10}}{5}$.
故选:D.
点评 本题考查椭圆的标准方程和简单性质,利用直线和椭圆有交点可得判别式大于或等于0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.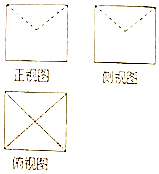 某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,两条虚线互相垂直,则该几何体的体积是( )
 某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,两条虚线互相垂直,则该几何体的体积是( )| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{3}$ |
8.从正五边形的5个顶点中随机选择3个顶点,则以它们作为顶点的三角形是锐角三角形的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
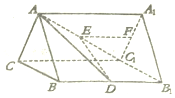 在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C为矩形,D,E,F分别是线段BB1,AC1,A1C1的中点.
在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C为矩形,D,E,F分别是线段BB1,AC1,A1C1的中点.