题目内容
5.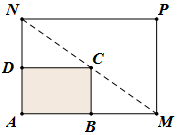 如图所示,某小区内有一矩形花坛,现将这一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.
如图所示,某小区内有一矩形花坛,现将这一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.(Ⅰ)设DN=x米,BM=y米,矩形AMPN的面积为z米2,试用x,y表示z;
(Ⅱ)当DN的长度是多少时,矩形花坛AMPN的面积最小?并求出最小值.
分析 (1)由相似得到xy=6,即可用x,y表示z;
(Ⅱ)化简矩形的面积,利用基本不等式,即可求得结论.
解答 解:(1)由相似得到$\frac{x}{3}=\frac{2}{y}$,∴xy=6…(2分)
∴面积z=(x+2)(y+3)…(4分)
(2)z=(x+2)(y+3)=(x+2)($\frac{6}{x}$+3)=3x+$\frac{12}{x}$+12≥24…(6分)
当且仅当3x=$\frac{12}{x}$,即x=2时,z有最小值24,
故DN的长为2米时,矩形AMPN的面积最小,最小值为24平方米…(8分)
点评 本题考查根据题设关系列出函数关系式,考查利用基本不等式求最值,解题的关键是确定矩形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.设数列{an}的通项公式an=ncos$\frac{nπ}{3}$,其前n项和为Sn,则S2016=( )
| A. | 2016 | B. | -2016 | C. | 1008 | D. | -1008 |
16.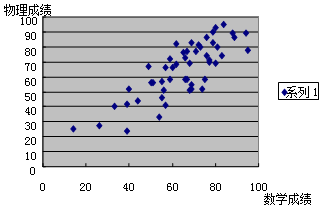 在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到如下散点图,用回归直线$\hat y=bx+a$近似刻画其关系,根据图形,b的数值最有可能是( )
在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到如下散点图,用回归直线$\hat y=bx+a$近似刻画其关系,根据图形,b的数值最有可能是( )
 在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到如下散点图,用回归直线$\hat y=bx+a$近似刻画其关系,根据图形,b的数值最有可能是( )
在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到如下散点图,用回归直线$\hat y=bx+a$近似刻画其关系,根据图形,b的数值最有可能是( )| A. | 0 | B. | 1.55 | C. | 0.45 | D. | -0.24 |
17.有5名高中优秀毕业生回母校成都7中参加高2015级励志成才活动,到3个班去做学习经验交流,则每个班至少去一名的不同分派方法种数为( )
| A. | 200 | B. | 180 | C. | 150 | D. | 280 |
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED是以BD为直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED是以BD为直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD. 一个几何体的三视图如图所示,图中矩形均为边长是1的正方形弧线为四分之一圆,则该几何体的体积是$1-\frac{π}{6}$.
一个几何体的三视图如图所示,图中矩形均为边长是1的正方形弧线为四分之一圆,则该几何体的体积是$1-\frac{π}{6}$.