题目内容
若α为锐角,且sinα:sin
=8:5,则cosα的值为( )
| α |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:二倍角的正弦
专题:三角函数的求值
分析:由已知可得5sinα=8sin
,两边平方后利用二倍角公式化简可得25cos2α-32cosα+7=0,又α为锐角,即可解得cosα的值.
| α |
| 2 |
解答:
解:∵sinα:sin
=8:5,
∴可得:5sinα=8sin
,两边平方可得:25-25cos2α=64×
,
∴可得:25cos2α-32cosα+7=0,α为锐角,
∴可得:cosα=1(舍去)或
,
故选:D.
| α |
| 2 |
∴可得:5sinα=8sin
| α |
| 2 |
| 1-cosα |
| 2 |
∴可得:25cos2α-32cosα+7=0,α为锐角,
∴可得:cosα=1(舍去)或
| 7 |
| 25 |
故选:D.
点评:本题主要考查了二倍角的余弦公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
复数
的共轭复数对应的点位于( )
| 1-i |
| 2-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
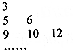 设{an}是集合{2s+2t|0≤s<t,且s、t∈Z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列{an}中的各项按照上小下大、左小右大的原则写成如图所示的三角形数阵,则a99=
设{an}是集合{2s+2t|0≤s<t,且s、t∈Z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列{an}中的各项按照上小下大、左小右大的原则写成如图所示的三角形数阵,则a99=