题目内容
11.定义在[0,+∞)上的函数f(x),当x∈[0,2]时,f(x)=4(|x-1|-1),且对任意实数 x∈[2n-2,2n+1-2](n∈N*,n≥2),都有f(x)=$\frac{1}{2}$f($\frac{x}{2}$-1),若方程f(x)-log a x=0有且仅有三个实根,则实数a的取值范围是( )| A. | [$\frac{\sqrt{10}}{10}$,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{\sqrt{10}}{10}$,$\frac{\sqrt{2}}{2}$) | C. | ($\frac{1}{10}$,$\frac{1}{2}$) | D. | [$\frac{1}{10}$,$\frac{1}{2}$) |
分析 作出y=f(x)和y=logax的函数图象,根据图象交点个数列不等式组,解出a即可.
解答 解:作出y=f(x)的函数图象如图所示: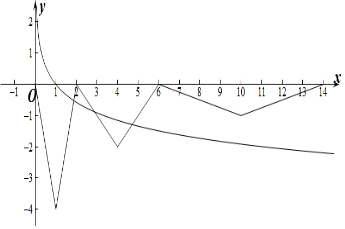
∵方程f(x)-log a x=0有且仅有三个实根,
∴y=f(x)与y=logax的函数图象有三个交点,
当a>1时,显然两图象只有1个交点,不符合题意;
当0<a<1时,若两图象有3个交点,
则$\left\{\begin{array}{l}{lo{g}_{a}4>-2}\\{lo{g}_{a}10<-1}\end{array}\right.$,解得$\frac{1}{10}$<a<$\frac{1}{2}$.
故选C.
点评 本题考查了方程解的个数与函数图象的关系,属于中档题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
6.己知x、y∈R,i是虚数单位,若x+yi与$\frac{2+i}{1+i}$互为共轭复数,则x+y=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
3.执行如图所示的程序框图,如果输人的x=-10.则输出的y=( )


| A. | 0 | B. | 1 | C. | 8 | D. | 27 |
 如图,将正六边形ABCDEF中的一半图形ABCD绕AD翻折到AB1C1D,使得∠B1AF=60°.G是BF与AD的交点.
如图,将正六边形ABCDEF中的一半图形ABCD绕AD翻折到AB1C1D,使得∠B1AF=60°.G是BF与AD的交点.