题目内容
7.在正四面体S-ABC中,若P为棱SC的中点,那么异面直线PB与SA所成的角的余弦值等于( )| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{33}}}{6}$ |
分析 取AC中点O,连结PO,BO,∠BPO是异面直线PB与SA所成的角,由此能求出异面直线PB与SA所成的角的余弦值.
解答 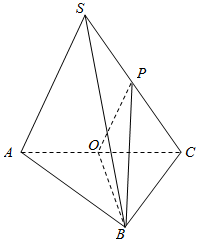 解:取AC中点O,连结PO,BO,设正四面体S-ABC的棱长为2,
解:取AC中点O,连结PO,BO,设正四面体S-ABC的棱长为2,
则PO∥SA,且PO=$\frac{1}{2}$SA=1,BO=BP=$\sqrt{4-1}$=$\sqrt{3}$,
∴∠BPO是异面直线PB与SA所成的角,
cos∠BPO=$\frac{P{O}^{2}+P{B}^{2}-B{O}^{2}}{2PO•PB}$=$\frac{1+3-3}{2×1×\sqrt{3}}$=$\frac{\sqrt{3}}{6}$.
∴异面直线PB与SA所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
故选:A.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
15.若实数x,y满足约束条件$\left\{\begin{array}{l}{-1≤x-y≤1}\\{1≤x+y≤3}\end{array}\right.$,则z=2x+y的取值范围是( )
| A. | [0,6] | B. | [1,6] | C. | [1,5] | D. | [2,4] |
2.设x>0,y>0,且2x+y=20,则lgx+lgy的最大值是( )
| A. | 50 | B. | 2 | C. | 1+lg5 | D. | 1 |
16.已知函数f(x)=x3-ax+1(a∈R),则下列结论正确的是( )
| A. | ?a∈R,f(x)是偶函数 | B. | ?a∈R,f(x)是奇函数 | ||
| C. | ?a∈R,f(x)在R上是增函数 | D. | ?a∈R,f(x)在R上是增函数 |