Question

设向量，,

（1）若，求的值；

（2）设函数，求的最大值，并指出对应的值．

Answer 1

 解：(1)由|a|²＝(sin x)²＋sin²x＝4sin²x，

|b|²＝cos²x＋sin²x＝1，及|a|＝|b|，得4sin²x＝1.

又x∈[0，]，从而sin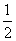 x＝，所以x＝.                      (2)f(x)＝a·b＝sin x·cos x＋sin²x＝sin 2x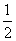－cos 2x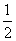＋＝sin(2x－)＋，

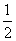当x＝∈[0，]时，sin(2x－)取最大值1.

所以的最大值为.