题目内容
已知一个圆锥的底面圆的半径为1，体积为
π，则该圆锥的侧面积为 ．
2
| ||
| 3 |
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：根据圆锥的体积计算出圆锥的高，以及圆锥的母线，进而求出圆锥的侧面积．
解答：
解：设圆锥的高为h，底面半径为r，
∵圆锥的底面半径为1，体积是
π，
∴
π×h=
πh=
π，
即h=2
，
∴圆锥的母线长l=
=3，
∴圆锥的侧面积S=πrl=3×π=3π，
故答案为：3π．
∵圆锥的底面半径为1，体积是
2
| ||
| 3 |
∴
| 1 |
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
即h=2
| 2 |
∴圆锥的母线长l=
12+(2
|
∴圆锥的侧面积S=πrl=3×π=3π，
故答案为：3π．
点评：本题主要考查圆锥的体积和侧面积的计算，要求熟练掌握圆锥的体积和侧面积公式．
练习册系列答案
综合自测系列答案
相关题目
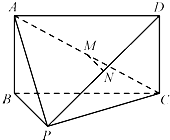如图，在四棱锥P-ABCD中，四边形ABCD为矩形，AB⊥BP，M、N分别为AC、PD的中点．求证：
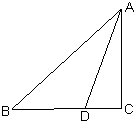如图，在Rt△ABC（C为直角）中，D为BC边上的一个三等分点（靠近点C），则tan∠BAD的最大值为已知函数f（x）=sin（2x+φ），其中φ为实数，且f（x）≤f（
）对x∈R恒成立．记P=f（
），Q=f（
），R=f（
），则P，Q，R的大小关系是（ ）
| 2π |
| 9 |
| 2π |
| 3 |
| 5π |
| 6 |
| 7π |
| 6 |
| A、R＜P＜Q |
| B、Q＜R＜P |
| C、P＜Q＜R |
| D、Q＜P＜R |