题目内容
8.函数f(x)=$\frac{ln(-{x}^{2}+2x+3)}{\sqrt{1-x}}$+x0的定义域为( )| A. | (-1,1) | B. | (-1,1) | C. | (-1,0)∪(0,1) | D. | (-1,0)∪(0,3) |
分析 函数f(x)=$\frac{ln(-{x}^{2}+2x+3)}{\sqrt{1-x}}$+x0有意义,只需$\left\{\begin{array}{l}{-{x}^{2}+2x+3>0}\\{1-x>0}\\{x≠0}\end{array}\right.$,解不等式即可得到所求定义域.
解答 解:函数f(x)=$\frac{ln(-{x}^{2}+2x+3)}{\sqrt{1-x}}$+x0有意义,
只需$\left\{\begin{array}{l}{-{x}^{2}+2x+3>0}\\{1-x>0}\\{x≠0}\end{array}\right.$即$\left\{\begin{array}{l}{-1<x<3}\\{x<1}\\{x≠0}\end{array}\right.$,
即-1<x<1且x≠0,
故定义域为(-1,0)∪(0,1).
故选:C.
点评 本题考查函数的定义域的求法,注意运用对数函数的定义和根式、分式的含义及零次幂函数的定义,考查运算能力,属于基础题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
13.原点到直线y=-$\frac{1}{2}$x+$\frac{5}{2}$的距离为( )
| A. | 1 | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
 已知函数f(x)=1+$\frac{x-|x|}{4}$.
已知函数f(x)=1+$\frac{x-|x|}{4}$.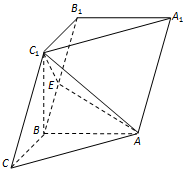 如图在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=BC1=$\sqrt{2}$,AB=CC1=2,点E在棱BB1上.
如图在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=BC1=$\sqrt{2}$,AB=CC1=2,点E在棱BB1上.