题目内容
如图所示, 在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
,![]()
![]() .
.
(1)若点![]() 分别为棱
分别为棱![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2) 请根据下列要求设计切割和拼接方法:要求用平行于三棱柱![]() 的某一条侧棱的平面去截此三棱柱,切开后的两个几何体再拼接成一个长方体. 简单地写出一种切割和拼接方法,
的某一条侧棱的平面去截此三棱柱,切开后的两个几何体再拼接成一个长方体. 简单地写出一种切割和拼接方法,
并写出拼接后的长方体的表面积(不必计算过程).

(1)证法一:以点![]() 为原点,分别以
为原点,分别以![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,依题意得
,依题意得![]() 、
、
![]() .
.
∴![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .
.
![]()
![]()

∴![]() .
.
∴![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
∴![]() 平面
平面![]() .
.
证法二:连结![]() ,
,
![]()
![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .
.
![]()
![]() ,
,![]() 分别为棱
分别为棱![]() 的中点,
的中点,
∴![]() .
.
![]() ,
,
∴Rt△![]() Rt△
Rt△![]() .
.
∴![]() .
.
![]() ,
,
∴![]() .
.

∴![]() .
.
![]()
![]()
∴![]()
![]() ,
,
∴![]() 平面
平面![]() .
.
∴![]() .
.
![]() ,
,
∴![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
∴![]() .
.
同理可证![]() .
.
![]() ,
,
∴![]() 平面
平面![]() .
.
(2)切割拼接方法一:如图甲所示,分别以![]() 的中点
的中点![]() 所确定的平面为截面,把三棱柱
所确定的平面为截面,把三棱柱![]() 切开后的两个几何体再拼接成一个长方体(该长方体的一个底面为长方形
切开后的两个几何体再拼接成一个长方体(该长方体的一个底面为长方形![]() 如图①所示,),此时所拼接成的长方体的表面积为16.
如图①所示,),此时所拼接成的长方体的表面积为16.


图甲 图①
切割拼接方法二:如图乙所示,设![]() 的中点分别为
的中点分别为![]() ,以四点
,以四点![]() 所确定的平面为截面,把三棱柱
所确定的平面为截面,把三棱柱![]() 切开后的两个几何体再拼接成一个长方体(该长方体的一个底面为正方形
切开后的两个几何体再拼接成一个长方体(该长方体的一个底面为正方形![]() ),此时所拼接成的长方体的表面积为
),此时所拼接成的长方体的表面积为![]() .
.


图乙 图②

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案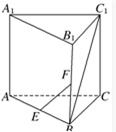 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、60° | C、90° | D、120° |
 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AB=2,BC=1,
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AB=2,BC=1, 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=BC=4,AC=3,AB=5.
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=BC=4,AC=3,AB=5.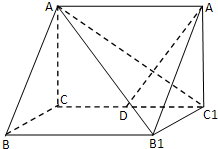 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AB=2,BC=1,
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AB=2,BC=1, 如图所示,在三棱柱ABC-A1B1C1中,E,F分别为AB,AC的中点,平面B1C1FE将三棱柱分成两部分,求这两部分的体积之比.
如图所示,在三棱柱ABC-A1B1C1中,E,F分别为AB,AC的中点,平面B1C1FE将三棱柱分成两部分,求这两部分的体积之比.