题目内容

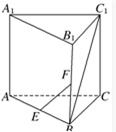如图所示，在三棱柱ABC-A₁B₁C₁中，AA₁⊥底面ABC，AB=BC=AA₁，∠ABC=90°，点E、F分别是棱AB、BB₁的中点，则直线EF和BC₁所成的角是（　　）

A、45°

B、60°

C、90°

D、120°

分析：先将EF平移到AB₁，再利用中位线进行平移，使两条异面直线移到同一点，得到所成角，求之即可．

解答：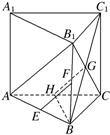

解：连接AB₁，易知AB₁∥EF，连接B₁C交BC₁于点
G，取AC的中点H，连接GH，则GH∥AB₁∥EF．设
AB=BC=AA₁=a，连接HB，在三角形GHB中，易
知GH=HB=GB=

a，故两直线所成的角即为∠HGB=60°．
故选B

点评：本题主要考查了异面直线及其所成的角，平移法是研究异面直线所成的角的最常用的方法，属于基础题．

练习册系列答案

1加1阅读好卷系列答案

如图所示，在三棱柱ABC-A₁B₁C₁中，H是正方形AA₁B₁B的中心 $数学公式$ 平面AA₁B₁B且 $数学公式$ ．
（1）求异面直线AC与A₁B₁所成角的余弦值；
（2）求二面角A-A₁C₁-B₁的正弦值．

如图所示，在三棱柱ABC－A′B′C′中，点E、F、H、K分别为AC′、CB′、A′B、B′C′的中点，G为△ABC的重心.从K、H、G、B′中取一点作为P，使得该棱柱恰有2条棱与平面PEF平行，则P为(　　).

(A)K (B)H (C)G (D)B′

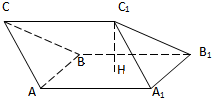如图所示，在三棱柱ABC-A1B1C1中，H是正方形AA1B1B的中心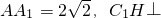平面AA1B1B且．（1）求异面直线AC与A1B1所成角的余弦值；（2）求二面角A-A1C1-B1的正弦值．