题目内容
 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AB=2,BC=1,AA1=
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AB=2,BC=1,AA1=| 3 |
(1)画出该三棱柱的三视图,并标明尺寸;
(2)求三棱锥A1-AB1C1的体积;
(3)若D是棱CC1的中点,则当点E在棱AB何处时,DE∥平面AB1C1?并证明你的结论.
分析:(1)根据三视图的画法规则:“长对正,宽相等,高平齐”即可画出;
(2)通过等积变形及三棱锥与同底等高的三棱柱的体积关系即可得出;
(3)通过面面平行即可得到线面平行.
(2)通过等积变形及三棱锥与同底等高的三棱柱的体积关系即可得出;
(3)通过面面平行即可得到线面平行.
解答:解:(1)三视图如图所示:
(2)在Rt△ABC中,AB=2,BC=1,∴由勾股定理得AC=
.
又∵AA1=
,AA1⊥平面ABC,∴矩形ACC1A1为正方形.
∴VA1-AB1C1=VA-A1B1C1=
VABC-A1B1C1=
×
×
×1×
=
.
(3)当点E为棱AB的中点时,DE∥平面AB1C1.
证明如下:
如图,取BB1的中点F,连EF、DF、DE,
∵D、E、F分别为CC1、AB、BB1的中点,
∴EF∥AB1.
∵AB1?平面AB1C1,EF?平面AB1C1,
∴EF∥平面AB1C1.
同理可证FD∥平面AB1C1.
∵EF∩FD=F,
∴平面EFD∥平面AB1C1.
∵DE?平面EFD,
∴DE∥平面AB1C1.

(2)在Rt△ABC中,AB=2,BC=1,∴由勾股定理得AC=
| 3 |
又∵AA1=
| 3 |
∴VA1-AB1C1=VA-A1B1C1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
(3)当点E为棱AB的中点时,DE∥平面AB1C1.
证明如下:
如图,取BB1的中点F,连EF、DF、DE,
∵D、E、F分别为CC1、AB、BB1的中点,
∴EF∥AB1.
∵AB1?平面AB1C1,EF?平面AB1C1,
∴EF∥平面AB1C1.
同理可证FD∥平面AB1C1.

∵EF∩FD=F,
∴平面EFD∥平面AB1C1.
∵DE?平面EFD,
∴DE∥平面AB1C1.
点评:熟练掌握三视图的画法规则、等积变形及利用面面平行证明线面平行是解题的关键.

练习册系列答案
相关题目
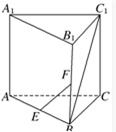 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、60° | C、90° | D、120° |
 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心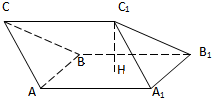 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心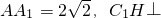 平面AA1B1B且
平面AA1B1B且 .
.
