题目内容
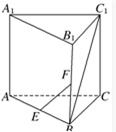
 如图所示,在三棱柱ABC-A1B1C1中,E,F分别为AB,AC的中点,平面B1C1FE将三棱柱分成两部分,求这两部分的体积之比.
如图所示,在三棱柱ABC-A1B1C1中,E,F分别为AB,AC的中点,平面B1C1FE将三棱柱分成两部分,求这两部分的体积之比.分析:设棱柱的底面积为S,高为h,根据截面EB1C1F将三棱柱分成两部分,一部分是三棱台AEF-A1B1C1,求得三棱台的体积,再用间接法求得另一部分的体积,计算两部分的体积比值.
解答:解:截面EB1C1F将三棱柱分成两部分,一部分是三棱台AEF-A1B1C1,
另一部分是一个不规则几何体,故可以利用棱柱的体积减去棱台的体积求得.
设棱柱的底面积为S,高为h,则△AEF的面积为
S,
∵V1=VAEF-A1B1C1=
(
+S+
)h=
Sh,
剩余的不规则几何体的体积为V2=V-V1=Sh-
Sh=
Sh,
∴两部分的体积之比为V1:V2=7:5
另一部分是一个不规则几何体,故可以利用棱柱的体积减去棱台的体积求得.
设棱柱的底面积为S,高为h,则△AEF的面积为
| 1 |
| 4 |
∵V1=VAEF-A1B1C1=
| 1 |
| 3 |
| S |
| 4 |
| S |
| 2 |
| 7 |
| 12 |
剩余的不规则几何体的体积为V2=V-V1=Sh-
| 7 |
| 12 |
| 5 |
| 12 |
∴两部分的体积之比为V1:V2=7:5
点评:本题考查了棱柱与棱台的体积计算,求解要细心.

练习册系列答案
相关题目
 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、60° | C、90° | D、120° |
 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心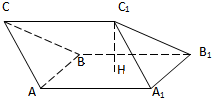 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心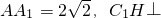 平面AA1B1B且
平面AA1B1B且 .
.
