题目内容
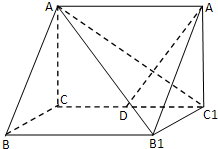 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AB=2,BC=1,AA1=
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AB=2,BC=1,AA1=| 6 |
(Ⅰ)证明:A1D⊥平面AB1C1;
(Ⅱ)求平面A1B1A与平面AB1C1所成的锐二面角的余弦值.
分析:(Ⅰ) 由已知,AA1⊥平面ABC,∠ACB=90°,证出B1C1⊥AA1C1C,从而得B1C1⊥A1D;在矩形AA1C1C中,利用△ACC1~△DC1A1,证出A1D⊥AC1,由线面垂直的判定定理即可证明:A1D⊥平面AB1C1.
(Ⅱ)在(Ⅰ)的基础上,设垂足(即为A1D与AC1的交点)为H,过A1作AB1的垂线,垂足为G,连GH,有三垂线定理逆定理,可证∠A1GH为二面角A1-AB1-C1的平面角,再解三角形A1GH即可获解.
(Ⅱ)在(Ⅰ)的基础上,设垂足(即为A1D与AC1的交点)为H,过A1作AB1的垂线,垂足为G,连GH,有三垂线定理逆定理,可证∠A1GH为二面角A1-AB1-C1的平面角,再解三角形A1GH即可获解.
解答: 解:(Ⅰ)∵∠ACB=90°,∴BC⊥AC.
解:(Ⅰ)∵∠ACB=90°,∴BC⊥AC.
∵三棱柱ABC-A1B1C1中,CC1⊥平面ABC.∴BC⊥CC1,
∵AC∩CC1=C,∴BC⊥平面ACC1A1.
∵A1D?平面ACC1A1,∴BC⊥A1D,而BC∥B1C1,则B1C1⊥A1D.
在Rt△ACC1与Rt△DC1A1中,
=
=
,∴△ACC1~△DC1A1,
∴∠AC1C=∠DA1C1.∴∠AC1C+∠C1DA1=90°.即A1D⊥AC1.
∵B1C1∩AC1=C1,∴A1D⊥平面AB1C1.
(Ⅱ)如图,设A1D∩AC1=H,过A1作AB1的垂线,垂足为G,连GH,
∵A1D⊥平面AB1C1,∴AB1⊥A1D,∴AB1⊥平面A1GH∴∠A1GH为二面角A1-AB1-C1的平面角.
在Rt△AA1B1中,AA1=
,A1B1=2,∴AB1=
,∴A1G=
=
;
在Rt△AA1C1中,AA1=
,A1C1=
,∴AC1=3,∴A1H=
=
.
∴在Rt△A1GH中,sin∠A1GH=
=
=
,cos∠A1GH=
.
故锐二面角A1-AB1-C1的余弦值为
.
即平面A1B1A与平面AB1C1所成的锐二面角的余弦值为
.
 解:(Ⅰ)∵∠ACB=90°,∴BC⊥AC.
解:(Ⅰ)∵∠ACB=90°,∴BC⊥AC.∵三棱柱ABC-A1B1C1中,CC1⊥平面ABC.∴BC⊥CC1,
∵AC∩CC1=C,∴BC⊥平面ACC1A1.
∵A1D?平面ACC1A1,∴BC⊥A1D,而BC∥B1C1,则B1C1⊥A1D.
在Rt△ACC1与Rt△DC1A1中,
| AC |
| CC1 |
| DC1 |
| AC1 |
| ||
| 2 |
∴∠AC1C=∠DA1C1.∴∠AC1C+∠C1DA1=90°.即A1D⊥AC1.
∵B1C1∩AC1=C1,∴A1D⊥平面AB1C1.
(Ⅱ)如图,设A1D∩AC1=H,过A1作AB1的垂线,垂足为G,连GH,
∵A1D⊥平面AB1C1,∴AB1⊥A1D,∴AB1⊥平面A1GH∴∠A1GH为二面角A1-AB1-C1的平面角.
在Rt△AA1B1中,AA1=
| 6 |
| 10 |
| AA1•A1B1 |
| AB1 |
2
| ||
| 5 |
在Rt△AA1C1中,AA1=
| 6 |
| 3 |
| AA1•A1C1 |
| AC1 |
| 2 |
∴在Rt△A1GH中,sin∠A1GH=
| A1H |
| A1G |
5
| ||
2
|
| ||
| 6 |
| ||
| 6 |
故锐二面角A1-AB1-C1的余弦值为
| ||
| 6 |
即平面A1B1A与平面AB1C1所成的锐二面角的余弦值为
| ||
| 6 |
点评:本题主要考查二面角的计算,直线和平面垂直的性质、判定,考查学生空间想象能力,计算能力、转化能力.空间问题平面化,是解决空间问题最核心的思想方法..

练习册系列答案
相关题目
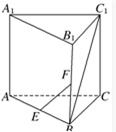 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、60° | C、90° | D、120° |
 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心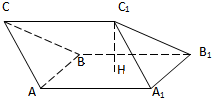 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心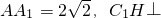 平面AA1B1B且
平面AA1B1B且 .
.
