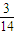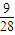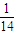题目内容
△ABC中A，B为锐角sinA-sinB=
，cosA-cosB=
．
（1）试通过计算判断△ABC的形状．
（2）求角A，B的值．
1-
| ||
| 2 |
| ||
| 2 |
（1）试通过计算判断△ABC的形状．
（2）求角A，B的值．
分析：（1）由条件可得
sin（A+
）=
sin（B+
），又A＜B，可得 A+
=π-（B+
），求得 A+B=
，故△ABC为直角三角形．
（2）把两个已知的等式平方相加可得 cos（A-B）=
，可得 A-B=-
，再由（1）A+B=
，从而求得A、B的值．
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
（2）把两个已知的等式平方相加可得 cos（A-B）=
| ||
| 2 |
| π |
| 6 |
| π |
| 2 |
解答：解：（1）∵△ABC中，A，B为锐角sinA-sinB=
，cosA-cosB=
，
∴sinA+cosA=sinB+cosB，即
sin（A+
）=
sin（B+
），又A＜B，
∴A+
=π-（B+
），∴A+B=
，故△ABC为直角三角形．
（2）把两个已知的等式平方相加可得 cos（A-B）=
，∴A-B=-
，
再由（1）A+B=
，
∴A=
，B=
．
1-
| ||
| 2 |
| ||
| 2 |
∴sinA+cosA=sinB+cosB，即
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
∴A+
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
（2）把两个已知的等式平方相加可得 cos（A-B）=
| ||
| 2 |
| π |
| 6 |
再由（1）A+B=
| π |
| 2 |
∴A=
| π |
| 6 |
| π |
| 3 |
点评：本题主要考查同角三角函数的基本关系的应用，已知三角函数值求角的大小，属于中档题．
练习册系列答案
相关题目
α，平面ABC与平面α所成的锐二面角为θ，AD⊥α，则下列结论中正确的是( )
α,平面ABC与平面α所成的锐二面角为θ,AD⊥α,则下列结论中正确的是( )
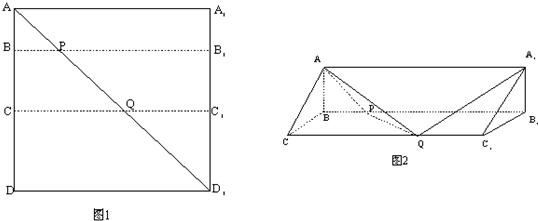
如图，在边长为12的正方形A1 AA′A1′中，点B、C在线段AA′上，且AB = 3，BC = 4，作BB1∥AA1，分别交A1A1′、AA1′于点B1、P；作CC1∥AA1，分别交A1A1′、AA1′于点C1、Q；将该正方形沿BB1、CC1折叠，使得A′A1′ 与AA1重合，构成如图所示的三棱柱ABC—A1B1C1，在三棱柱ABC—A1B1C1中， （Ⅰ）求证：AB⊥平面BCC1B1； （Ⅱ）求面PQA与面ABC所成的锐二面角的大小．（Ⅲ）求面APQ将三棱柱ABC—A1B1C1分成上、下两部分几何体的体积之比．
