题目内容
6.由①y=2x+5是一次函数;②y=2x+5的图象是一条直线;③一次函数的图象是一条直线.写一个“三段论”形式的正确推理,则作为大前提、小前提和结论的分别是( )| A. | ②①③ | B. | ③②① | C. | ①②③ | D. | ③①② |
分析 本题考查的知识点是演绎推理中三段论的概念,由三段论:①y=2x+5是一次函数;②y=2x+5的图象是一条直线;③一次函数的图象是一条直线;我们易得大前提是③,小前提是①,结论是②.则易得答案.
解答 解:三段论:
①y=2x+5是一次函数;
②y=2x+5的图象是一条直线;
③一次函数的图象是一条直线;
大前提是③,
小前提是①,
结论是②.
故排列的次序应为:③①②,
故选:D.
点评 演绎推理的主要形式就是由大前提、小前提推出结论的三段论推理.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
8.命题:“对于任意角θ,cos4θ-sin4θ=cos2θ”的证明过程:“cos4θ-sin4θ=(cos2θ-sin2θ)(cos2θ+sin2θ)=cos2θ-sin2θ=cos2θ”应用了( )
| A. | 分析法 | B. | 综合法 | ||
| C. | 综合法与分析法结合使用 | D. | 演绎法 |
17.设集合A={x|-1<x<2},B={x|y=lg(x-1)},则A∩(∁RB)=( )
| A. | [-1,2) | B. | [2,+∞) | C. | (-1,1] | D. | [-1,+∞) |
14.已知点P(4,-3)是角α终边上一点,则下列三角函数值中正确的是( )
| A. | tanα=-$\frac{4}{3}$ | B. | tanα=-$\frac{3}{4}$ | C. | sinα=-$\frac{4}{5}$ | D. | cosα=$\frac{3}{5}$ |
16.若不等式|8x+9|<7和不等式ax2+bx>2的解集相等,则实数a,b的值分别为( )
| A. | a=-8,b=-10 | B. | a=-4,b=-9 | C. | a=-1,b=9 | D. | a=-1,b=2 |
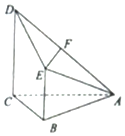 已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.
已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.