题目内容
9.已知椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1,F1,F2是椭圆的两个焦点,则|F1F2|=2$\sqrt{7}$.分析 求出椭圆的a,b,再由c=$\sqrt{{a}^{2}-{b}^{2}}$,即可得到所求焦距2c.
解答 解:椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的a=4,b=3,
c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{7}$,
即有|F1F2|=2$\sqrt{7}$.
故答案为:2$\sqrt{7}$.
点评 本题考查椭圆的方程,主要考查椭圆的焦距的求法,考查运算能力,属于基础题.

练习册系列答案
相关题目
4.一个棱长为12的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体的体积最大值是( )
| A. | 16$\sqrt{2}$ | B. | 6$\sqrt{2}$ | C. | 12$\sqrt{2}$ | D. | 32$\sqrt{2}$ |
1.已知一正三棱台上底边长为3,下底边长为6,高为3,则此三棱台体积为( )
| A. | $\frac{{63\sqrt{3}}}{4}$ | B. | $\frac{{21\sqrt{3}}}{4}$ | C. | $\frac{{45\sqrt{3}}}{4}$ | D. | $\frac{{15\sqrt{3}}}{4}$ |
18.若集合M={-2,-1,0,1,2},N={x|x2<3},则M∩N等于( )
| A. | ∅ | B. | {-1,1} | C. | {-2,2} | D. | {-1,0,1} |
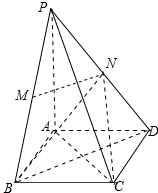 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点