题目内容
已知奇函数y=f（x）（x∈R）在[0，+∞）为增函数，则满足不等式f（x）+f（2x+1）＞0的x的集合为 ．
考点：奇偶性与单调性的综合
专题：函数的性质及应用
分析：根据奇函数的性质判断出函数在R单调性，再利用函数是奇函数，将不等式转化为f（2x+1）＞f（-x），列出不等式求出x的范围．
解答：
解：∵奇函数y=f（x）（x∈R）在[0，+∞）为增函数，
∴函数y=f（x）（x∈R）在（-∞，0）为增函数，
即奇函数y=f（x）在R上为增函数，
由f（x）+f（2x+1）＞0得，f（2x+1）＞-f（x）=f（-x），
∴2x+1＞-x，解得x＞-
，
则不等式的解集是{x|x＞-
}，
故答案为：{x|x＞-
}．
∴函数y=f（x）（x∈R）在（-∞，0）为增函数，
即奇函数y=f（x）在R上为增函数，
由f（x）+f（2x+1）＞0得，f（2x+1）＞-f（x）=f（-x），
∴2x+1＞-x，解得x＞-
| 1 |
| 3 |
则不等式的解集是{x|x＞-
| 1 |
| 3 |
故答案为：{x|x＞-
| 1 |
| 3 |
点评：本题主要考查函数奇偶性和单调性的应用，主要判断出在定义域上的单调性．
练习册系列答案
相关题目
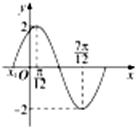已知函数f（x）=Asin（ωx+φ）在一个周期内的图象如图所示．