题目内容

14．$\overrightarrow{z}$是复数z的共轭复数，若复数z满足$\frac{i}{\overline{z}}$=1+i，则z=．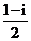

分析 直接利用复数的代数形式的混合运算，以及共轭复数的概念，即可求出．

解答 解：∵$\frac{i}{\overline{z}}$=1+i，
∴$\overline{z}$=$\frac{i}{1+i}$=$\frac{1+i}{2}$，
∴z=$\frac{1-i}{2}$，
故答案为：$\frac{1-i}{2}$．

点评 本题考查复数的基本运算，复数的基本概念，考查计算能力．

练习册系列答案
相关题目
11．设i是虚数单位，则复数z=（$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i）2的共轭复数$\overline{z}$=（　　）
A．-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$iB．-$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$iC．$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$iD．$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i
5．已知公差不为0的等差数列{an}的首项a1=a（a＞0），该数列的前n项和为Sn，且$\frac{1}{{a}_{1}}$，$\frac{1}{{a}_{2}}$，$\frac{1}{{a}_{4}}$成等比数列．
（Ⅰ）求数列{an}的通项公式及Sn；
（Ⅱ）设bn=$\frac{1}{{S}_{n}}$，cn=$\frac{1}{{a}_{{2}^{n-1}}}$，且Bn，Cn分别为数列{bn}，{cn}的前n项和，当n≥2时，试比较Bn与Cn的大小．
2．已知曲线C的极坐标方程是ρ=2sinθ，直线l的参数方程是$\left\{\begin{array}{l}{x=-\frac{3}{5}t+2}\\{y=\frac{4}{5}t}\end{array}\right.$（t为参数）
（Ⅰ）将曲线C的极坐标方程化为直角坐标方程；
（Ⅱ）设直线l与x轴的交点是M，N是曲线C上一动点，求MN的最大值．
9．已知各项均为正数的数列{an}的前n项和Sn满足8Sn=a${\;}_{n}^{2}$+4an+3（∈N*），且a1＜3．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足bn=$\frac{{a}_{n}+3-3n}{{2}^{n-1}}$，设{bn}的前n项和为Tn，若不等式（-1）nλ＜Tn+$\frac{n}{{2}^{n-1}}$对一切n∈N*恒成立，求实数λ的取值范围．
19．阅读如图所示的程序框图，运行相应的程序，则输出的结果是（　　）
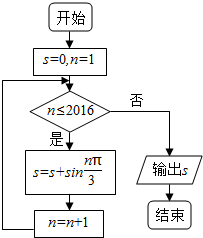
A．-$\sqrt{3}$B．0C．$\sqrt{3}$D．$336\sqrt{3}$
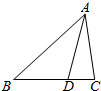6．已知四面体ABCD的外接球球心O在棱CD上，$AB=\sqrt{3}$，CD=2，则A、B两点在四面体ABCD的外接球上的球面距离是$\frac{2π}{3}$．
3．△ABC中，∠A=120°，∠A的平分线AD交边BC于D，且AB=2，CD=2DB，则AD的长为$\frac{4}{3}$．
4．如图所示，在△ABC中，D为BC边上的一点，且BD=2DC，若$\overrightarrow{AC}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$（m，n∈R），则$\frac{n}{m}$=-3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网