题目内容
11.设i是虚数单位,则复数z=($\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i)2的共轭复数$\overline{z}$=( )| A. | -$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | B. | -$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i | C. | $\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | D. | $\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i |
分析 利用复数的运算法则、共轭复数的定义即可得出.
解答 解:z=($\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i)2=$\frac{1}{4}$-$\frac{3}{4}$-$\frac{\sqrt{3}}{2}$i=-$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i,
则$\overline{z}$=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,
故选:A.
点评 本题考查了复数的运算法则、共轭复数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
2.log42-log48等于( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
6.已知等差数列{an}的前n项Sn,若$\overrightarrow{OA}$=a10$\overrightarrow{OB}$+a2006$\overrightarrow{OC}$-3$\overrightarrow{OD}$且A、B、C、D四点共面(原点O不在此四点所确定的面内),则S2015=( )
| A. | 2015 | B. | 2016 | C. | 4030 | D. | 4032 |
20.已知f(x)=sin(ωx+φ)(ω>0,|φ|<π)的图象相邻的对称轴之间的距离为2π,将其向左平移$\frac{π}{2}$个单位,所得函数图象与g(x)=cos(ωx+$\frac{π}{3}$)重合,则φ的值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{7π}{12}$ | D. | $\frac{2π}{3}$ |
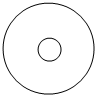 某家庭游戏中有这样一个“投币”活动,活动道具是如图所示的半径为10cm的圆形纸板,纸板上有一个相同圆心、半径为2cm的小圆,现让家庭中的每名成员向此纸板抛掷一枚半径为1cm的硬币,使硬币整体随机落在纸板内,若硬币落下后与小圆圆面(不包含边界)无公共点则中奖,否则不中奖.
某家庭游戏中有这样一个“投币”活动,活动道具是如图所示的半径为10cm的圆形纸板,纸板上有一个相同圆心、半径为2cm的小圆,现让家庭中的每名成员向此纸板抛掷一枚半径为1cm的硬币,使硬币整体随机落在纸板内,若硬币落下后与小圆圆面(不包含边界)无公共点则中奖,否则不中奖.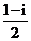 .
.