题目内容
7.已知α,β是锐角,α+β≠$\frac{π}{2}$,且满足3sinβ=sin(2α+β).(1)求证:tan(α+β)=2tanα;
(2)求证:tanβ$≤\frac{\sqrt{2}}{4}$,并求等号成立时tanα与tanβ的值.
分析 (1)把条件3sinβ=sin(2α+β)中的角都用所要证明的结论中的角表示为3sin[(α+β)-α]=sin[(α+β)+α];再利用两角和与差的正弦公式展开,整理即可证明结论;
(2)先由(1)得tanβ=tan[(α+β)-α]=$\frac{tan(α+β)-tanα}{1+tan(α+β)tanα}=\frac{tanα}{1+2ta{n}^{2}α}=\frac{1}{\frac{1}{tanα}+2tanα}$,再利用基本不等式求出分母的最值;即可求出tanβ的最大值,并求出其取最大值时tanα的值.
解答 证明:(1)由3sinβ=sin(2α+β)得:
3sin[(α+β)-α]=sin[(α+β)+α],
∴3sin(α+β)cosα-3cos(α+β)sinα=sin(α+β)cosα+cos(α+β)sinα,
得sin(α+β)cosα=2cos(α+β)sinα,
∵α、β是锐角,α+β≠$\frac{π}{2}$,
∴$\frac{sin(α+β)cosα}{cos(α+β)cosα}=\frac{2cos(α+β)sinα}{cos(α+β)cosα}$,得tan(α+β)=2tanα;
(2)∵tanβ=tan[(α+β)-α]=$\frac{tan(α+β)-tanα}{1+tan(α+β)tanα}=\frac{tanα}{1+2ta{n}^{2}α}=\frac{1}{\frac{1}{tanα}+2tanα}$,
又∵α是锐角,
∴$\frac{1}{tanα}+2tanα$≥2$\sqrt{\frac{1}{tanα}•2tanα}=2\sqrt{2}$,当且仅当$\frac{1}{tanα}$=2tanα时取等号,
此时tanα=$\frac{\sqrt{2}}{2}$.
故tanβ≤$\frac{1}{2\sqrt{2}}=\frac{\sqrt{2}}{4}$.
∴当tanα=$\frac{\sqrt{2}}{2}$,tanβ=$\frac{\sqrt{2}}{4}$时等号成立.
点评 本题考查两角和与差的正切函数,在三角恒等式的证明中,一般都是把已知条件与所证结论相结合,即要看条件,又要分析条件和结论之间的关系,是中档题.

| A. | $\frac{5}{12}$ | B. | $\frac{5}{18}$ | C. | $\frac{5}{6}$ | D. | $\frac{5}{36}$ |
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
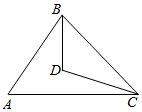 如图,D为△ABC内一点,并且满足AB=CD=4,∠A+∠BDC=180°,试确定S△ABC-S△BDC的最大值.
如图,D为△ABC内一点,并且满足AB=CD=4,∠A+∠BDC=180°,试确定S△ABC-S△BDC的最大值.