题目内容
12.设$|{\overrightarrow a}|=12,|{\overrightarrow b}|=9,\overrightarrow a•\overrightarrow b=-54\sqrt{2}$,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )| A. | 45° | B. | 60° | C. | 120° | D. | 135° |
分析 利用向量夹角公式即可得出.
解答 解:$cos<\overrightarrow{a},\overrightarrow{b}>$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{-54\sqrt{2}}{12×9}$=$-\frac{\sqrt{2}}{2}$,
∴向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为135°.
故选:D.
点评 本题考查了向量夹角公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
2.已知复数Z=$\frac{1-\sqrt{3}i}{(\sqrt{3}+i)^{2}}$,$\overline{Z}$是Z的共轭复数,则Z•$\overline{Z}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 2 | D. | 4 |
7.函数y=sinx的图象( )
| A. | 关于点$({\frac{π}{2},1})$对称 | B. | 关于直线x=π对称 | C. | 关于点(π,0)对称 | D. | 关于y轴对称 |
4.已知两点A(3,0),B(0,4),动点P(x,y)在线段AB上运动,则xy的最大值为( )
| A. | $\frac{12}{5}$ | B. | $\frac{144}{49}$ | C. | 3 | D. | 4 |
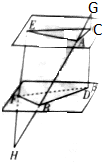 如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.
如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.