题目内容
17.给出下列命题:①存在实数x,使$sinx+cosx=\frac{3}{2}$;
②若α,β是第一象限角,且α>β,则cosα<cosβ;
③函数$y=\frac{{{{sin}^2}x-sinx}}{sinx-1}$是奇函数;
④函数$y=|sinx-\frac{1}{2}|$的周期是π;
⑤函数y=ln|x-1|的图象与函数y=-2cos(πx)(-2≤x≤4)的图象所有交点的横坐标之和等于6.
其中正确命题的序号是⑤(把正确命题的序号都填上)
分析 ①由sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)≤$\sqrt{2}$判断命题错误;
②当α,β是第一象限角且α>β时cosα<cosβ不一定成立;
③根据定义域不关于原点对称判断函数y不是奇函数;
④由正弦函数的图象与性质知函数$y=|sinx-\frac{1}{2}|$的周期是2π;
⑤由图象变化的法则和余弦函数的特点作出函数的图象,由对称性可得答案.
解答 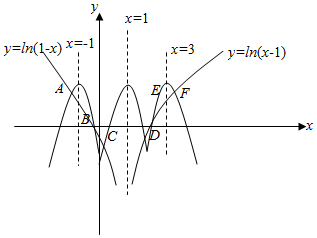 解:对于①,sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)≤$\sqrt{2}$<$\frac{3}{2}$,
解:对于①,sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)≤$\sqrt{2}$<$\frac{3}{2}$,
∴不存在实数x,使$sinx+cosx=\frac{3}{2}$,①错误;
对于②,α,β是第一象限角,且α>β,
则cosα<cosβ不一定成立,
如α=405°,β=45°时,cos405°=cos45°,②错误;
对于③,函数$y=\frac{{{{sin}^2}x-sinx}}{sinx-1}$=sinx,
其中sinx≠1,即x≠$\frac{π}{2}$+2kπ,k∈Z,
∴y不是奇函数,③错误;
对于④,由正弦函数的图象与性质知,
函数$y=|sinx-\frac{1}{2}|$的周期是2π,④错误;
对于⑤,由图象变化的法则可知:
y=lnx的图象作关于y轴的对称后和原来的一起构成y=ln|x|的图象,
向右平移1个单位得到y=ln|x-1|的图象,再把x轴上方的图象不动,
下方的图象对折上去可得g(x)=ln|x-1||的图象;
又f(x)=-2cosπx的周期为T=2,如图所示:
两图象都关于直线x=1对称,且共有6个交点,
由中点坐标公式可得:xA+xB=-2,xD+xC=2,xE+xF=6,故所有交点的横坐标之和为6,⑤正确;
综上,正确的命题是⑤.
故答案为:⑤.
点评 本题考查了命题真假的判断与应用问题,涉及知识点多,综合性强.


| A. | 57 | B. | 42 | C. | 26 | D. | 11 |
 已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( )| A. | 36π | B. | 30π | C. | 29π | D. | 20π |

 中,角
中,角 、
、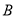 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且 .
. ,求
,求 ;
;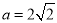 ,且
,且 的面积为
的面积为 ,求
,求 的周长.
的周长. .
. 时,求不等式
时,求不等式 的解集;
的解集; 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.