题目内容
已知函数f(x)=
-log2
.
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性并证明;
(3)讨论f(x)在区间(0,1)上的单调性.
| 1 |
| x |
| 1+x |
| 1-x |
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性并证明;
(3)讨论f(x)在区间(0,1)上的单调性.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)根据使函数解析式有意义的原则,构造关于x的不等式组,解得函数f(x)的定义域;
(2)先分析函数f(x)的定义域关于原点对称,再判断f(-x)与f(x)的关系,进而根据函数奇偶性的定义判断f(x)的奇偶性并证明;
(3)结合反比例函数的单调性,对数函数的单调性,复合函数单调性“同增异减”的原则,结合减-增=减的性质,可判断出f(x)在区间(0,1)上的单调性.
(2)先分析函数f(x)的定义域关于原点对称,再判断f(-x)与f(x)的关系,进而根据函数奇偶性的定义判断f(x)的奇偶性并证明;
(3)结合反比例函数的单调性,对数函数的单调性,复合函数单调性“同增异减”的原则,结合减-增=减的性质,可判断出f(x)在区间(0,1)上的单调性.
解答:
解:(1)由题可知
,解得x∈(-1,0)∪(0,1),
所以函数f(x)的定义域为(-1,0)∪(0,1). (4分)
(2)函数f(x)是奇函数.
事实上,函数f(x)的定义域关于原点对称,
且对定义域内的任意x,有
f(-x)=
-log2
=-(
-log2
)=-f(x),
∴函数f(x)是奇函数. (8分)
(3)由反比例函数的性质可得:
y=
=
-1在区间(0,1)上为增函数,
故y=log2
在区间(0,1)上为增函数,
又由y=
在区间(0,1)上为减增函数,
故f(x)在区间(0,1)上为减函数.(12分)
|
所以函数f(x)的定义域为(-1,0)∪(0,1). (4分)
(2)函数f(x)是奇函数.
事实上,函数f(x)的定义域关于原点对称,
且对定义域内的任意x,有
f(-x)=
| 1 |
| -x |
| 1-x |
| 1+x |
| 1 |
| x |
| 1+x |
| 1-x |
∴函数f(x)是奇函数. (8分)
(3)由反比例函数的性质可得:
y=
| 1+x |
| 1-x |
| -2 |
| x-1 |
故y=log2
| 1+x |
| 1-x |
又由y=
| 1 |
| x |
故f(x)在区间(0,1)上为减函数.(12分)
点评:本题考查的知识点是函数的单调性,函数的奇偶性,函数的定义域,是函数图象和性质的综合应用,难度中档.

练习册系列答案
相关题目
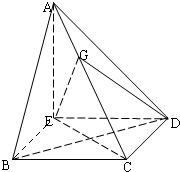 如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6
如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6