题目内容
如图,已知直线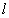 与抛物线
与抛物线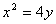 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为
(2,0).
(I) 若动点M满足 ,求点M的轨迹C;
,求点M的轨迹C;
(II)若过点B的直线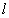 ′(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
′(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
解析:(I)由 ,
, ∴直线l的斜率为
∴直线l的斜率为 ,
,
故l的方程为 ,∴点A坐标为(1,0)
,∴点A坐标为(1,0)
设 则
则 ,
,
由 得
得 
整理,得
∴点M的轨迹为以原点为中心,焦点在x轴上,长轴长为 ,短轴长为2的椭圆
,短轴长为2的椭圆
(II)如图,由题意知直线l的斜率存在且不 为零,设l方程为y=k(x-2)(k≠0)①
为零,设l方程为y=k(x-2)(k≠0)①
|

练习册系列答案
相关题目

 ,随机变量X表示
,随机变量X表示 .
. (x)=ex+2x2-3x.
(x)=ex+2x2-3x. 时,若关于x的不等式f(x)≥
时,若关于x的不等式f(x)≥ x2+ (a-
x2+ (a- 3)x+1恒成立,试求实数a的取值范围.
3)x+1恒成立,试求实数a的取值范围. ,双曲线
,双曲线 的焦点是椭圆的顶点, 顶点是椭圆的焦点,则双曲线的离心率为( )
的焦点是椭圆的顶点, 顶点是椭圆的焦点,则双曲线的离心率为( ) B.
B. C.2 D.3
C.2 D.3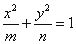 的离心率为2,且一个焦点与抛物线
的离心率为2,且一个焦点与抛物线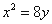 的焦点相同,则此双曲线的方程为______.
的焦点相同,则此双曲线的方程为______. ,则( )
,则( ) B.
B. C.
C.  D.
D.
 :方程
:方程 有两个不等的负实根,
有两个不等的负实根, :方程
:方程 无实根.若
无实根.若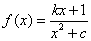 (
(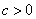 且
且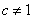 ,
,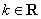 )恰有一个极大值点和一个极小值点,其中一个是
)恰有一个极大值点和一个极小值点,其中一个是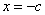 .
.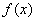 的另一个极值点;
的另一个极值点;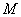 和极小值
和极小值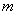 ,并求
,并求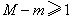 时
时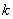 的取值范围.
的取值范围. -
-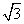 cos2x+
cos2x+ ,x∈R.
,x∈R. 上的最大值和最小值.
上的最大值和最小值.