题目内容
15.已知随机变量x服从正态分布N(3,σ2),且P(x≤4)=0.84,则P(2<x<4)=( )| A. | 0.84 | B. | 0.68 | C. | 0.32 | D. | 0.16 |
分析 根据对称性,由P(x≤4)=0.84的概率可求出P(x<2)=P(x>4)=0.16,即可求出P(2<x<4).
解答 解:∵P(x≤4)=0.84,
∴P(x>4)=1-0.84=0.16
∴P(x<2)=P(x>4)=0.16,
∴P(2<x<4)=P(x≤4)-P(x<2)=0.84-0.16=0.68
故选B.
点评 本题主要考查正态分布曲线的特点及曲线所表示的意义,注意根据正态曲线的对称性解决问题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
5.在复平面内,复数g(x)满足$z({1+i})=|{1+\sqrt{3}i}|$,则z的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.已知点A(1,1),B(2,1),C(1,2),若λ∈[-1,2],μ∈[2,3],则|λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$|的取值范围是( )
| A. | [2,10] | B. | [$\sqrt{5}$,$\sqrt{13}$] | C. | [1,5] | D. | [2,$\sqrt{13}$] |
20.若函数f(x)=xsin2016+cosx,则该函数的图象在点(2016,f(2016))处切线的斜率等于( )
| A. | -2sin2016 | B. | sin2016 | C. | 0 | D. | 2sin2016 |
4.已知tanα=-$\frac{1}{3}$.则$\frac{1}{co{s}^{2}α}$等于( )
| A. | 9 | B. | 10 | C. | $\frac{1}{9}$ | D. | $\frac{10}{9}$ |
5.如图是一个程序框图,则输出的S的值是( )


| A. | -1 | B. | 0 | C. | 8 | D. | 9 |
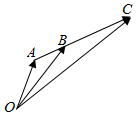 已知A(2,3),B(5,4),连接AB并延长至C,使得AC=3AB,求C点的坐标.(提示:如图所示,$\overrightarrow{OC}$=$\overrightarrow{OA}$+3$\overrightarrow{AB}$)
已知A(2,3),B(5,4),连接AB并延长至C,使得AC=3AB,求C点的坐标.(提示:如图所示,$\overrightarrow{OC}$=$\overrightarrow{OA}$+3$\overrightarrow{AB}$)