题目内容
 已知:如图,在棱长为1的正方体ABCD-A1B1C1D1中,M是A1B上的点,A1M=
已知:如图,在棱长为1的正方体ABCD-A1B1C1D1中,M是A1B上的点,A1M=| 1 |
| 3 |
| 1 |
| 3 |
(I) 求证:直线MN是异面直线A1B与B1D1的公垂线;
(Ⅱ) 求直线MN与平面ABCD所成角的正弦值.
考点:直线与平面所成的角,异面直线的判定
专题:空间位置关系与距离,空间角
分析:(I)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能证明直线MN是异面直线A1B与B1D1的公垂线.
(Ⅱ)由
=(-
,
,
),平面ABCD的法向量
=(0,0,1),利用向量法能求出直线MN与平面ABCD所成角的正弦值.
(Ⅱ)由
| MN |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| n |
解答:
(I)证明: 以D为原点,DA为x轴,DC为y轴,DD1为z轴,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,
建立空间直角坐标系,
A1(1,0,1),B(1,1,0),
=(0,1,-1),
D1(0,0,1),B1(1,1,1),
=(-1,-1,0),
设M(x,y,z),N(a,b,c),
=(x-1,y,z-1),
=(a-1,b-1,c-1),
∵M是A1B上的点,A1M=
A1B,N是B1D1上的点,B1N=
B1D1,
∴(x-1,y,z-1)=(0,
,-
),∴M(1,
,
),
(a-1,b-1,c-1)=(-
,-
,0),∴N(
,
,1),
∴
=(-
,
,
),
∴
•
=0,
•
=0,
∴MN⊥A1B,MN⊥B1D1.
又MN∩A1B=M,MN∩B1D1=M,
∴直线MN是异面直线A1B与B1D1的公垂线.
(Ⅱ)解:设直线MN与平面ABCD所成角为θ,
∵
=(-
,
,
),平面ABCD的法向量
=(0,0,1),
∴sinθ=|cos<
,
>|=|
|=
.
∴直线MN与平面ABCD所成角的正弦值为
.
 以D为原点,DA为x轴,DC为y轴,DD1为z轴,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
A1(1,0,1),B(1,1,0),
| A1B |
D1(0,0,1),B1(1,1,1),
| B1D1 |
设M(x,y,z),N(a,b,c),
| A1M |
| B1M |
∵M是A1B上的点,A1M=
| 1 |
| 3 |
| 1 |
| 3 |
∴(x-1,y,z-1)=(0,
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
(a-1,b-1,c-1)=(-
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴
| MN |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴
| MN |
| A1B |
| MN |
| B1D1 |
∴MN⊥A1B,MN⊥B1D1.
又MN∩A1B=M,MN∩B1D1=M,
∴直线MN是异面直线A1B与B1D1的公垂线.
(Ⅱ)解:设直线MN与平面ABCD所成角为θ,
∵
| MN |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| n |
∴sinθ=|cos<
| MN |
| n |
| ||||
|
| ||
| 3 |
∴直线MN与平面ABCD所成角的正弦值为
| ||
| 3 |
点评:本题考查异面直线的公垂线的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
某算法的程序如图所示,若输入x=2,则电脑屏上显示的结果为( )


| A、16 | B、4 | C、y=0 | D、0 |
 如图,直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.
如图,直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.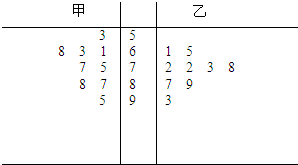 某班级甲乙两个小组各9名同学的期中考试数学成绩 (单位:分)的茎叶图如图
某班级甲乙两个小组各9名同学的期中考试数学成绩 (单位:分)的茎叶图如图