题目内容
设s,t为正整数,两直线l1:| t |
| 2s |
| t |
| 2s |
分析:首先由l1与l2的方程求得交点的横坐标,即x1,再由点斜式求得过点(0,t)和(xn-1,0)的直线l的方程,然后求l与l2的交点横坐标,最后代入xn求得x2,x3…从而归纳出数列an通项公式xn.
解答:解:∵直线l1与l2的交点是(s,
),即x1=s.过点 (0,t) 和 ( xn-1,0 )的直线 l 方程是y=-(
)x+t,
与l2的交点的横坐标是x=
,
即 xn═
(n≥2),
∴x2=
=
s,x3=
s,…
猜想xn=
s.
故答案为:xn=
s.
| t |
| 2 |
| t |
| xn-1 |
与l2的交点的横坐标是x=
| 2s•xn-1 |
| 2s+xn-1 |
即 xn═
| 2s•xn-1 |
| 2s+xn-1 |
∴x2=
| 2s•s |
| 2s+s |
| 2 |
| 3 |
| 2 |
| 4 |
猜想xn=
| 2 |
| n+1 |
故答案为:xn=
| 2 |
| n+1 |
点评:本题主要考查由递推公式推导数列的通项公式,其中渗透了不完全归纳法思想,属于基础题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
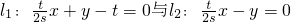 的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn).则数列xn通项公式xn=________.
的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn).则数列xn通项公式xn=________.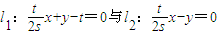 的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn).则数列xn通项公式xn= .
的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn).则数列xn通项公式xn= . 的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn).
的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn).