题目内容
设s,t为正整数,两直线 的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn).
的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn).(1)求数列{xn}通项公式;
(2)求数列{xnxn+1}的前n项和Sn.
【答案】分析:(1)根据两直线 的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn),可得
的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn),可得 ,取倒数,即可得到
,取倒数,即可得到 为等差数列,且首项为
为等差数列,且首项为 ,公差为
,公差为 ,从而可求数列{xn}通项公式;
,从而可求数列{xn}通项公式;
(2)根据数列{xnxn+1}通项的特点,裂项求和,即可得到结论.
解答:解:(1)依题意,∵两直线 的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn),
的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn),
∴
∴
∴ 为等差数列,且首项为
为等差数列,且首项为 ,公差为
,公差为
∴
∴
(2)
∴ =
=
点评:本题考查直线的交点、数列通项的求法,考查数列的求和,综合性较强,确定数列的通项是关键.
 的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn),可得
的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn),可得 ,取倒数,即可得到
,取倒数,即可得到 为等差数列,且首项为
为等差数列,且首项为 ,公差为
,公差为 ,从而可求数列{xn}通项公式;
,从而可求数列{xn}通项公式;(2)根据数列{xnxn+1}通项的特点,裂项求和,即可得到结论.
解答:解:(1)依题意,∵两直线
 的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn),
的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn),∴

∴

∴
 为等差数列,且首项为
为等差数列,且首项为 ,公差为
,公差为
∴

∴

(2)

∴
 =
=
点评:本题考查直线的交点、数列通项的求法,考查数列的求和,综合性较强,确定数列的通项是关键.

练习册系列答案
相关题目
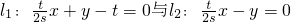 的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn).则数列xn通项公式xn=________.
的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn).则数列xn通项公式xn=________.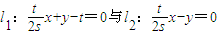 的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn).则数列xn通项公式xn= .
的交点是(x1,y1),对于正整数n(n≥2),过点(0,t)和(xn-1,0)的直线与直线l2的交点记为(xn,yn).则数列xn通项公式xn= .