题目内容
3．曲线y=e-x+1在点（0，2）处的切线与直线y=0和x=0围成三角形的面积为2．分析 求函数的导数，利用导数求出函数的切线方程，结合三角形的面积公式进行求解即可．
解答 解：函数的导数f′（x）=-e-x，
则f′（0）=-1，则切线方程为y-2=-x，即y=-x+2，
切线与x轴的交点为（2，0），与y轴的交点为（0，2），
∴切线与直线y=0和x=0围成三角形的面积S=$\frac{1}{2}×2×2=2$，
故答案为：2
点评 本题主要考查三角形面积的计算，求函数的导数，利用导数的几何意义求出切线方程是解决本题的关键．
练习册系列答案
相关题目
14．已知函数f（x）=$\frac{1}{3}$x3+ax2+2x+2的图象在点（x0，f（x0））处的切线与直线x+y+1=0垂直，则实数a的取值范围为（ ）
| A． | [-1，1] | B． | （-1，1） | C． | （-∞，-1]∪[1，+∞） | D． | （-∞，-1）∪（1，+∞） |
11．将函数f（x）=sin（2x+ϕ），$（|ϕ|＜\frac{π}{2}）$的图象沿x轴向左平移$\frac{π}{8}$个单位后，得到一个偶函数g（x）的图象，则函数g（x）的一个减区间为（ ）
| A． | $[{-\frac{π}{4}，\frac{π}{4}}]$ | B． | $[{-\frac{π}{2}，0}]$ | C． | $[{0，\frac{π}{2}}]$ | D． | $[{\frac{π}{4}，\frac{3π}{4}}]$ |
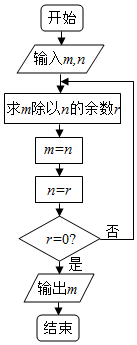如图程序框图的算法思路源于古希腊数学家欧几里得的“辗转相除法”，执行该程序框图，若输入的m，n分别为153，119，则输出的m=（ ）
8．复数$\frac{i}{1+i}$-$\frac{1}{2i}$的实部与虚部的和为（ ）
| A． | -$\frac{1}{2}$ | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{3}{2}$ |
