题目内容

2．如图，已知直三棱柱ABC-A′B′C′的底面为等边三角形，D是AA′上的点，E是B′C′的中点，且A′E∥平面DBC′，试判断点D在AA′上的位置，并给出证明．

分析 D点是AA′的中点．如图，取BC的中点O，连接EO，DO，欲证明A′E∥平面DBC′，只需推知A′E∥DO．所以证得四边形A′DOE为平行四边形即可．

解答 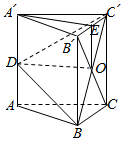解：D点是AA′的中点．理由如下：
如图，取BC的中点O，连接EO，DO，
∵直三棱柱ABC-A′B′C′的底面为等边三角形，E是B′C′的中点，
∴EO∥BB′∥AA′．
又∵A′E∥平面DBC′，
∴A′E∥DO．
∴四边形A′DOE是平行四边形，
∴A′D=EO，
∴D点是AA′的中点．

点评 本题考查了直线与平面平行的判定．对于平面外的一条直线，只需在平面内找到一条直线和这条直线平行，就可判定这条直线必和这个平面平行．即由线线平行得到线面平行．

练习册系列答案
相关题目
12．已知三个函数：①f（x）=x3，②f（x）=tanx，③f（x）=xsinx，其图象能将圆O：x2+y2=1的面积等分的函数的个数是（　　）
A．3B．2C．1D．0
13．已知数列{an}的前n项和为Sn，且a1=3，Sn+1-2Sn=1-n．
（I）求数列{an}的通项公式；
（Ⅱ）令bn=$\frac{{2}^{n-1}}{{a}_{n}{a}_{n+1}}$，求数列{bn}的前n项和Tn．
10．已知数列{an}满足[2-（-1）n]an+[2+（-1）n]an+1=1+（-1）n×3n，则a25-a1=300．
17．已知命题p：?x∈R，cosx＞1，则￢p是（　　）
A．?x∈R，cosx＜1B．?x∈R，cosx＜1C．?x∈R，cosx≤1D．?x∈R，cosx≤1
7．设集合A={（m1，m2，m3）|mi∈{-2，0，2}，i∈{1，2，3}}，则集合A满足条件：“2≤|m1|+|m2|+|m3|≤5”的元素个数为18．
14．在数列{an}中，a1=2，a2=4，且an+1=3an-2an-1（n≥2），设bn=log2${\;}^{（{a}_{n+1}-{a}_{n）}}$
（1）求证：数列{bn}为等差数列；
（2）求数列{$\frac{1}{{b}_{{\;}_{n}}{b}_{n+1}}$}的前n项和．
11．在△ABC中，A=$\frac{π}{3}$，|$\overrightarrow{AC}$|=m，m∈[1，2]，若对于任意实数t恒有|$\overrightarrow{AB}$-t$\overrightarrow{AC}$|≥|$\overrightarrow{BC}$|，则△ABC面积的最大值是（　　）
A．1B．$\sqrt{3}$C．2D．2$\sqrt{3}$
12．等差数列的第1项是7，第9项是1，则它的第5项是（　　）
A．2B．3C．4D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网