题目内容
在如图所示的几何体中, 四边形 是正方形,
是正方形, ,
, ,且
,且 ,
, ,
, .
.

(Ⅰ)若 与
与 交于点
交于点 ,求证:
,求证:  平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)
【解析】
试题分析:(Ⅰ)如图,取 中点
中点 ,连
,连 ,
, ,易得
,易得 ,且
,且 ,又由已知得,
,又由已知得, ,且
,且 ,所以四边形
,所以四边形 是平行四边形,所以
是平行四边形,所以 ,所以
,所以 平面
平面 ;(Ⅱ)建立空间直角坐标系,只需证明
;(Ⅱ)建立空间直角坐标系,只需证明 ,
, 即可. (Ⅲ)设平面
即可. (Ⅲ)设平面 的法向量为
的法向量为 由(Ⅱ)知
由(Ⅱ)知 ,
, ,
, ,易得
,易得 ,
,
又平面 的法向量为
的法向量为 ,所以可求得二面角
,所以可求得二面角 的余弦值为
的余弦值为
试题解析:(Ⅰ)如图,取 中点
中点 ,连
,连 ,
, , 在
, 在 中,因为
中,因为 分别是
分别是 的中点,
的中点,
所以 ,且
,且 ,又由已知得,
,又由已知得, ,且
,且 ,
,
所以 ,所以四边形
,所以四边形 是平行四边形,所以
是平行四边形,所以 3分
3分
又 平面
平面 ,
, 平面
平面 所以
所以 平面
平面 4分
4分
(Ⅱ)如图,以 为坐标原点建立空间直角坐标系
为坐标原点建立空间直角坐标系

则 ,
, ,
,
 ,
, , 2分
, 2分
所以 ,
,
 ,
,
所以 ,
,
且
所以 ,
, ; 4分
; 4分
又 ,所以
,所以 平面
平面 5分
5分
(Ⅲ)设平面 的法向量为
的法向量为
由(Ⅱ)知 ,
,
所以 ,令
,令 ,得
,得 2分
2分
又平面 的法向量为
的法向量为 3分
3分
设二面角 的大小为
的大小为 ,
, 是锐角
是锐角
则
所以二面角 的余弦值为
的余弦值为 5分
5分
考点:立体几何的综合应用

练习册系列答案
相关题目
 沿对角线
沿对角线 折成直二角后,下列命题正确的是( )
折成直二角后,下列命题正确的是( )



 的解集是 .
的解集是 .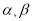 是两个不同的平面,以下说法正确的有 (填所有真命题的序号)
是两个不同的平面,以下说法正确的有 (填所有真命题的序号)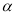 ,则m⊥
,则m⊥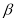 ,
,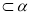 ,则
,则 的准线方程为
的准线方程为  :
: ,在圆周上随机取一点P,则P到直线
,在圆周上随机取一点P,则P到直线 的距离大于
的距离大于 的概率为 .
的概率为 .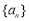 ,则“
,则“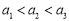 ”是“
”是“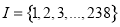 ,若
,若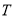 是
是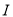 的子集且满足条件:当
的子集且满足条件:当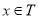 时,
时,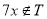 ,则集合
,则集合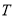 中元素的个数最多是( )
中元素的个数最多是( ) B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.