题目内容
12. 已知函数f(x)是R上的奇函数,且x>0时,f(x)=-x2+2x.
已知函数f(x)是R上的奇函数,且x>0时,f(x)=-x2+2x.(1)求f(x)的解析式;
(2)在如图的直角坐标系中画出函数求f(x)的图象,并求不等式f(x)<0的解集.
分析 (1)根据函数奇偶性的性质,利用对称性进行求解即可.
(2)画图,并由图象得到结论.
解答 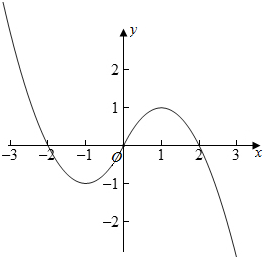 解:(1)设x<0,则-x>0,
解:(1)设x<0,则-x>0,
∴f(-x)=-(-x)2-2x=-x2-2x,
∵f(x)是R上的奇函数,
∴f(-x)=-f(x),f(0)=0,
∴f(x)=x2+2x,
∴f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2x,x≥0}\\{{x}^{2}+2x,x<0}\end{array}\right.$,
(2)其图象如图所示,
由图象可知,f(x)<0的解集为(-2,0)∪(2,+∞).
点评 本题考查函数解析式的求解,利用了奇函数的性质f(x)=-f(-x),以及函数图象的画法和不等式的解法,属于基础题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
2.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是A1B上一动点,则AP+D1P的最小值为( )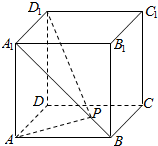

| A. | 2 | B. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ | C. | $2+\sqrt{2}$ | D. | $\sqrt{2+\sqrt{2}}$ |
20. 某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10m(如图所示),则旗杆的高度为( )
某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10m(如图所示),则旗杆的高度为( )
 某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10m(如图所示),则旗杆的高度为( )
某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10m(如图所示),则旗杆的高度为( )| A. | 10 m | B. | 30 m | C. | 10m | D. | 10m |
17.下列函数是幂函数的是( )
| A. | $y=2{x^{\frac{1}{2}}}$ | B. | y=x3+x | C. | y=2x | D. | $y={x^{\frac{1}{2}}}$ |
2.函数y=2|1+x|的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |