$\frac{{lg\sqrt{2}+lg3-lg\sqrt{10}}}{lg1.8}$=$\frac{1}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

4．$\frac{{lg\sqrt{2}+lg3-lg\sqrt{10}}}{lg1.8}$=$\frac{1}{2}$．

分析根据对数的运算性质计算即可．

解答解：$\frac{{lg\sqrt{2}+lg3-lg\sqrt{10}}}{lg1.8}$=$\frac{lg\frac{3\sqrt{2}}{\sqrt{10}}}{lg1.8}$=$\frac{\frac{1}{2}lg1.8}{lg1.8}$=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$

点评本题考查了对数的运算性质，属于基础题..

练习册系列答案

夺分A计划小学毕业升学总复习系列答案

小学毕业升学总复习金榜小状元系列答案

同步测评卷期末卷系列答案

小学生10分钟口算测试100分系列答案

相关题目

14．

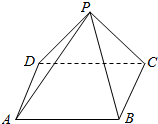已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$，侧面等腰三角形的顶角为30°，则从A点出发环绕面一周后回到A点的最短路程为（　　）

15．已知等差数列{a_n}中，S_n为其前n项和，且a₄=5，S₆=-39．
（1）求{a_n}的通项公式；
（2）求数列{a_n}的前n项和S_n的最小值．

12．

已知函数f（x）是R上的奇函数，且x＞0时，f（x）=-x²+2x．
（1）求f（x）的解析式；
（2）在如图的直角坐标系中画出函数求f（x）的图象，并求不等式f（x）＜0的解集．

19．下列四个图象中，是函数图象的是（　　）

9．已知函数$f（x）=\sqrt{-{x^2}+4x-3}$的定义域为M．
（1）求f（x）的定义域M；
（2）求当x∈M时，求函数g（x）=4^x-a•2^x+1（a为常数，且a∈R）的最小值．

16．已知$\overrightarrow a=（{1，-1，1}）$，则与向量$\overrightarrow a$共线的单位向量是（　　）

A．

$\overrightarrow n=±（{1，-1，1}）$

B．

$\overrightarrow n=±（{\frac{1}{3}，-\frac{1}{3}，\frac{1}{3}}）$

C．

$\overrightarrow n=±（{\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}）$

D．

$\overrightarrow n=±（{\frac{{\sqrt{3}}}{3}，-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}）$

13．已知a=log₃₆₅0.99、b=1.01³⁶⁵、c=0.99³⁶⁵，则a、b、c的大小关系为（　　）

14．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左右焦点F₁、F₂与椭圆短轴的一个端点构成边长为4的正三角形．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知过椭圆C上一点（x₀，y₀），与椭圆C相切的直线方程为$\frac{{{x_0}x}}{a^2}+\frac{{{y_0}y}}{b^2}$=1．过椭圆C上任意一点P作椭圆C的切线与直线F₁P的垂线F₁M相交于点M，求点M的轨迹方程；
（Ⅲ）若切线MP与直线x=-2交于点N，求证：$\frac{{|N{F_1}|}}{{|M{F_1}|}}$为定值．

试题分类