题目内容
如图,四棱锥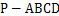 的底面
的底面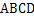 是平行四边形,
是平行四边形,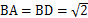 ,
,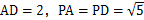 ,
,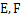 分别是棱
分别是棱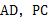 的中点.
的中点.
(1)证明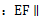 平面
平面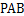 ;
;
(2)若二面角P-AD-B为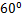 ,
,
①证明:平面PBC⊥平面ABCD
②求直线EF与平面PBC所成角的正弦值.

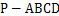 的底面
的底面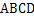 是平行四边形,
是平行四边形,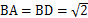 ,
,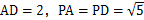 ,
,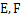 分别是棱
分别是棱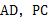 的中点.
的中点.(1)证明
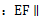 平面
平面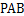 ;
;(2)若二面角P-AD-B为
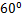 ,
,①证明:平面PBC⊥平面ABCD
②求直线EF与平面PBC所成角的正弦值.

(1)详见解析, (2)①详见解析,②

试题分析:(1)证明线面平行,一般利用线线平行进行证明.本题条件中的中点较多,所以取PB中点M,利用中位线性质找寻平行条件.因为F为PC中点,故MF//BC且MF=
 BC.由已知有BC//AD,BC=AD.又由于E为AD中点,因而MF//AE且MF=AE,故四边形AMFE为平行四边形,所以EF//AM,又AM
BC.由已知有BC//AD,BC=AD.又由于E为AD中点,因而MF//AE且MF=AE,故四边形AMFE为平行四边形,所以EF//AM,又AM 平面PAB,而EF
平面PAB,而EF 平面PAB,所以EF//平面PAB.,(2)①证明面面垂直,关键在一个面内找出另一平面的垂线.经分析BE
平面PAB,所以EF//平面PAB.,(2)①证明面面垂直,关键在一个面内找出另一平面的垂线.经分析BE 平面PBC.这是因为通过计算可得BE
平面PBC.这是因为通过计算可得BE PB, 又BC//AD,BE
PB, 又BC//AD,BE AD,从而BE
AD,从而BE BC,②求线面角,关键是找面的垂线,由①知BE
BC,②求线面角,关键是找面的垂线,由①知BE 平面PBC.所以
平面PBC.所以 EFB为直线EF与平面PBC所成的角,下面只需分别求出BE与EF的值即可.在三角形ABP中,可求得AM=
EFB为直线EF与平面PBC所成的角,下面只需分别求出BE与EF的值即可.在三角形ABP中,可求得AM= ,故EF=
,故EF= ,又BE=1,故在直角三角形EBF中,
,又BE=1,故在直角三角形EBF中, 所以,直线EF与平面PBC所成角的正弦值为
所以,直线EF与平面PBC所成角的正弦值为
证明(1)如图取PB中点M,连接MF,AM.因为F为PC中点,故MF//BC且MF=
 BC.由已知有BC//AD,BC=AD.又由于E为AD中点,因而MF//AE且MF=AE,故四边形AMFE为平行四边形,所以EF//AM,又AM
BC.由已知有BC//AD,BC=AD.又由于E为AD中点,因而MF//AE且MF=AE,故四边形AMFE为平行四边形,所以EF//AM,又AM 平面PAB,而EF
平面PAB,而EF 平面PAB,所以EF//平面PAB.
平面PAB,所以EF//平面PAB.
(2)①连接PE,BE.因为PA=PD,BA=BD,而E为AD中点,故PE
 AD,BE
AD,BE AD,所以
AD,所以 PEB为二面角P-AD-B的平面角.在三角形PAD中,由
PEB为二面角P-AD-B的平面角.在三角形PAD中,由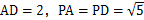 ,可解得PE=2.在三角形ABD中,由
,可解得PE=2.在三角形ABD中,由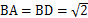 ,可解得BE=1.在三角形PEB中,PE="2," BE="1,"
,可解得BE=1.在三角形PEB中,PE="2," BE="1,"  ,由余弦定理,可解得PB=
,由余弦定理,可解得PB= ,从而
,从而 ,即BE
,即BE PB,又BC//AD,BE
PB,又BC//AD,BE AD,从而BE
AD,从而BE BC,因此BE
BC,因此BE 平面PBC.又BE
平面PBC.又BE 平面ABCD,所以平面PBC
平面ABCD,所以平面PBC 平面ABCD,②连接BF,由①知BE
平面ABCD,②连接BF,由①知BE 平面PBC.所以
平面PBC.所以 EFB为直线EF与平面PBC所成的角,由PB=
EFB为直线EF与平面PBC所成的角,由PB= ,PA=
,PA= ,AB=
,AB= 得
得 ABP为直角,而MB=
ABP为直角,而MB= PB=
PB= ,可得AM=
,可得AM= ,故EF=
,故EF= ,又BE=1,故在直角三角形EBF中,
,又BE=1,故在直角三角形EBF中, 所以,直线EF与平面PBC所成角的正弦值为
所以,直线EF与平面PBC所成角的正弦值为

练习册系列答案
相关题目
 中,侧面
中,侧面 为菱形,
为菱形, 的中点为
的中点为 ,且
,且 平面
平面

 ,
, 求三棱柱
求三棱柱 中,
中, 为矩形,平面
为矩形,平面 平面
平面

 问
问 为何值时,四棱锥
为何值时,四棱锥 与平面
与平面 夹角的余弦值.
夹角的余弦值. ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.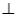 平面
平面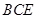 ;(2)点M在直线EF上,且
;(2)点M在直线EF上,且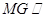 平面
平面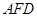 ,求平面ACH与平面ACM所成锐角的余弦值.
,求平面ACH与平面ACM所成锐角的余弦值.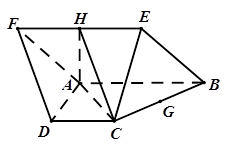

 中,
中, 底面
底面 ,
, ,E、F分别是棱
,E、F分别是棱 的中点.
的中点.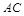 上的点
上的点 满足平面
满足平面 //平面
//平面 ,试确定点
,试确定点 ⊥A1C.
⊥A1C.
 A
A

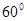 的菱形
的菱形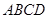 沿较短对角线
沿较短对角线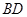 折成二面角
折成二面角 ,点
,点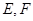 分别为
分别为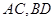 的中点,给出下列四个命题:
的中点,给出下列四个命题: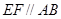 ;②
;②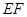 是异面直线
是异面直线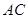 与
与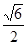 ;④
;④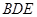 .
. 平面
平面 ,直线
,直线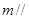 平面
平面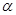 ,则
,则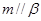 ;
;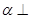 平面
平面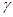 ,且平面
,且平面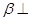 平面
平面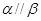 ;
;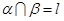 ,点
,点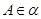 ,
,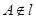 ,若直线
,若直线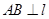 ,则
,则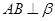 ;
;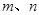 为异面直线,且
为异面直线,且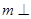 平面
平面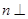 平面
平面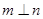 ,则
,则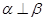 .
.