题目内容
将边长为2,锐角为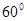 的菱形
的菱形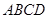 沿较短对角线
沿较短对角线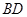 折成二面角
折成二面角 ,点
,点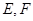 分别为
分别为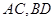 的中点,给出下列四个命题:
的中点,给出下列四个命题:
①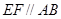 ;②
;②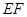 是异面直线
是异面直线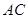 与
与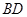 的公垂线;③当二面角
的公垂线;③当二面角 是直二面角时,
是直二面角时,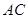 与
与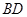 间的距离为
间的距离为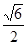 ;④
;④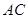 垂直于截面
垂直于截面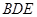 .
.
其中正确的是 (将正确命题的序号全填上).
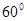 的菱形
的菱形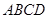 沿较短对角线
沿较短对角线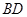 折成二面角
折成二面角 ,点
,点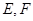 分别为
分别为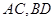 的中点,给出下列四个命题:
的中点,给出下列四个命题:①
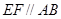 ;②
;②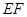 是异面直线
是异面直线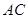 与
与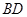 的公垂线;③当二面角
的公垂线;③当二面角 是直二面角时,
是直二面角时,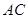 与
与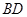 间的距离为
间的距离为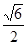 ;④
;④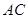 垂直于截面
垂直于截面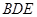 .
.其中正确的是 (将正确命题的序号全填上).
②③④
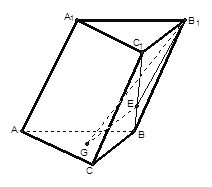
试题分析:如图可知①不正确;对于②连接AF、CF可知
 所以
所以 从而
从而 ,且
,且 ;同理连接BE,DE可得
;同理连接BE,DE可得 ,且
,且 ,所以EF是异面直线AC与BD的公垂线,故②正确;对于③,由②可知
,所以EF是异面直线AC与BD的公垂线,故②正确;对于③,由②可知 是二面角
是二面角 的平面角,所以
的平面角,所以 =900,那么在直角三角形AFC中,有
=900,那么在直角三角形AFC中,有 ,故知③正确;对于④,由②的过程可知其正确.
,故知③正确;对于④,由②的过程可知其正确.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
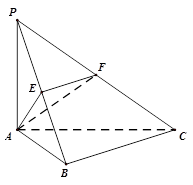
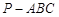 中,
中,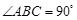 ,
,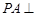 平面
平面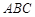 ,
,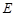 ,
,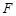 分别为
分别为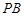 ,
, 的中点.
的中点.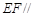 平面
平面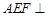 平面
平面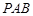 .
.
 CD=1,PD=
CD=1,PD= .
.
 ?
?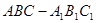 中,侧面
中,侧面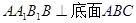 ,
,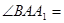
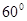 ,
,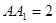 ,底面
,底面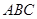 是边长为
是边长为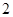 的正三角形,其重心为
的正三角形,其重心为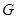 点,
点,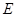 是线段
是线段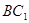 上一点,且
上一点,且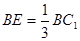 .
.
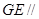 侧面
侧面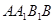 ;
;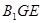 与底面
与底面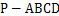 的底面
的底面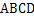 是平行四边形,
是平行四边形,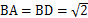 ,
,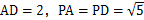 ,
,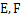 分别是棱
分别是棱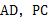 的中点.
的中点.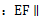 平面
平面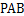 ;
;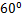 ,
,
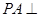 平面ABCD,AD//BC,
平面ABCD,AD//BC,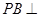 AC,
AC,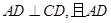
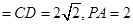 ,点M在线段PD上.
,点M在线段PD上.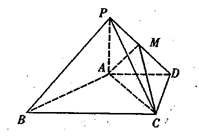
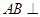 平面PAC;
平面PAC;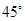 ,试确定点M的位置.
,试确定点M的位置.