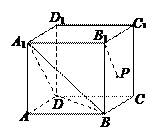题目内容
如图所示,在长方体OABC-O A
A B
B C
C 中,|OA|=2,|AB|=3,|AA
中,|OA|=2,|AB|=3,|AA |=2,E是BC的中点。
|=2,E是BC的中点。


(1)求直线AO 与B
与B E所成角的大小;
E所成角的大小;
(2)作O D⊥AC于D。求点O
D⊥AC于D。求点O 到点D的距离。
到点D的距离。
 A
A B
B C
C 中,|OA|=2,|AB|=3,|AA
中,|OA|=2,|AB|=3,|AA |=2,E是BC的中点。
|=2,E是BC的中点。

(1)求直线AO
 与B
与B E所成角的大小;
E所成角的大小;(2)作O
 D⊥AC于D。求点O
D⊥AC于D。求点O 到点D的距离。
到点D的距离。(1)AO 与B
与B E所成角的大小为arccos
E所成角的大小为arccos (2)
(2)
 与B
与B E所成角的大小为arccos
E所成角的大小为arccos (2)
(2)
如图所示,建立空间直角坐标系。
(1)由题设知,A(2,0,0),O (0,0,2),B
(0,0,2),B (2,3,2),E(1,3,0)。
(2,3,2),E(1,3,0)。
∴ =(-2,0,2),
=(-2,0,2), =(-1,0,-2)。
=(-1,0,-2)。
∴cos< ,
, >=
>= =-
=- 。
。
∴AO 与B
与B E所成角的大小为arccos
E所成角的大小为arccos 。
。
(2)由题意得 ⊥
⊥ ,
, //
// 。∵C(0,3,0)。设D(x,y,0),
。∵C(0,3,0)。设D(x,y,0),
∴O D=(x,y,-2),
D=(x,y,-2), =(x-2,y,0),
=(x-2,y,0), =(-2,3,0)。
=(-2,3,0)。
∴ ,∴
,∴ 。∴D(
。∴D( ,
, ,0)。
,0)。
∴|O D|=|
D|=| |=
|=
(1)由题设知,A(2,0,0),O
 (0,0,2),B
(0,0,2),B (2,3,2),E(1,3,0)。
(2,3,2),E(1,3,0)。∴
 =(-2,0,2),
=(-2,0,2), =(-1,0,-2)。
=(-1,0,-2)。∴cos<
 ,
, >=
>= =-
=- 。
。∴AO
 与B
与B E所成角的大小为arccos
E所成角的大小为arccos 。
。(2)由题意得
 ⊥
⊥ ,
, //
// 。∵C(0,3,0)。设D(x,y,0),
。∵C(0,3,0)。设D(x,y,0),∴O
 D=(x,y,-2),
D=(x,y,-2), =(x-2,y,0),
=(x-2,y,0), =(-2,3,0)。
=(-2,3,0)。∴
 ,∴
,∴ 。∴D(
。∴D( ,
, ,0)。
,0)。∴|O
 D|=|
D|=| |=
|=

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
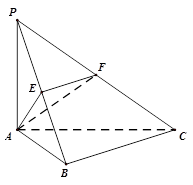
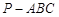 中,
中, ,
, 平面
平面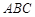 ,
,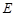 ,
,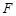 分别为
分别为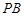 ,
, 的中点.
的中点. 平面
平面 平面
平面 .
.
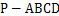 的底面
的底面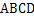 是平行四边形,
是平行四边形,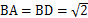 ,
,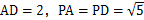 ,
,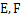 分别是棱
分别是棱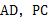 的中点.
的中点.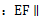 平面
平面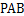 ;
;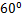 ,
,
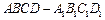 中,底面边长为
中,底面边长为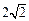 ,侧棱长为4,点
,侧棱长为4,点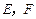 分别为棱
分别为棱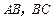 的中点,
的中点,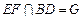 ,求点
,求点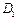 到平面
到平面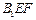 的距离
的距离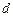 .
.
 中,
中, ,
, 面
面 ,
, ,求面
,求面 与面
与面 所成二面角的正切值.
所成二面角的正切值. ,
, 〉=
〉= .
.
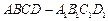 的棱长为1,点
的棱长为1,点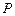 在侧面
在侧面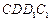 及其边界上运动,并且总保持
及其边界上运动,并且总保持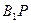 平行平面
平行平面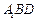 ,则动点P的轨迹的长度是 _______ .
,则动点P的轨迹的长度是 _______ .