题目内容
设函数f(x)=
,g(x)=
,对任意x1,x2∈(0,+∞),不等式kg(x1)≤(k+1)f(x2)恒成立,则正数k的取值范围是 .
| ex-2 |
| x |
| 2lnx |
| x |
考点:函数恒成立问题
专题:综合题,导数的综合应用
分析:利用导数性质求出f(x)min=
,g(x)max=g(e)=
.由对任意x1,x2∈(0,+∞),不等式kg(x1)≤(k+1)f(x2)恒成立,得到
≤(k+1)•
,由此能求出k的取值范围.
| 1 |
| e |
| 2 |
| e |
| 2k |
| e |
| 1 |
| e |
解答:
解:x>0时,∵f(x)=
,∴f′(x)=
,
∴函数在(0,1)上单调递减,在(1,+∞)上单调递增,
∴f(x)min=
.
∵g(x)=
,∴g′(x)=
,
令g′(x)=0,得x=e.
当x∈(0,e),g′(x)>0;当x∈(e,+∞)时,g′(x)<0.
∴g(x)max=g(e)=
.
∴对任意的x1,x2∈(0,+∞),f(x)min<g(x)max.
∵对任意x1,x2∈(0,+∞),不等式kg(x1)≤(k+1)f(x2)恒成立,
∴
≤(k+1)•
,解得k≤1
故答案为:(-∞,1].
| ex-2 |
| x |
| (x-1)ex-2 |
| x2 |
∴函数在(0,1)上单调递减,在(1,+∞)上单调递增,
∴f(x)min=
| 1 |
| e |
∵g(x)=
| 2lnx |
| x |
| 2(1-lnx) |
| x2 |
令g′(x)=0,得x=e.
当x∈(0,e),g′(x)>0;当x∈(e,+∞)时,g′(x)<0.
∴g(x)max=g(e)=
| 2 |
| e |
∴对任意的x1,x2∈(0,+∞),f(x)min<g(x)max.
∵对任意x1,x2∈(0,+∞),不等式kg(x1)≤(k+1)f(x2)恒成立,
∴
| 2k |
| e |
| 1 |
| e |
故答案为:(-∞,1].
点评:本题主要考查了导数在函数的单调性,最值求解中的应用,函考查数的恒成立问题的转化,本题具有一定的难度.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
函数f(x)=3x+x-3在区间(0,1)内的零点个数是( )
| A、3 | B、2 | C、1 | D、0 |
函数y=
的图象大致是( )
| 1 |
| x-sinx |
A、 |
B、 |
C、 |
D、 |
设函数f(x)=x2-12x+20,g(x)=f(x)+|f(x)|,则g(1)+g(2)+…+g(10)=( )
| A、0 | B、9 | C、12 | D、18 |
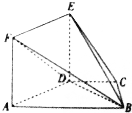 如图,在多面体ABCDEF中,平面ADEF⊥平面ABCD,AB∥DC,ADEF是正方形,已知BD=2AD=2,AB=2DC=
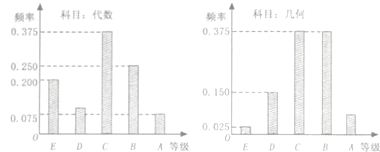
如图,在多面体ABCDEF中,平面ADEF⊥平面ABCD,AB∥DC,ADEF是正方形,已知BD=2AD=2,AB=2DC= 某校从参加某次数学能力测试的学生中中抽查36名学生,统计了他们的数学成绩(成绩均为整数且满分为120分),成绩的频率直方图如图所示,
某校从参加某次数学能力测试的学生中中抽查36名学生,统计了他们的数学成绩(成绩均为整数且满分为120分),成绩的频率直方图如图所示,