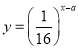题目内容
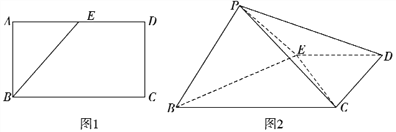
【题目】如图,在棱长为1的正方体![]() 中,点
中,点![]() 在
在![]() 上移动,点
上移动,点![]() 在
在![]() 上移动,
上移动,![]() ,连接
,连接![]() .
.

(1)证明:对任意![]() ,总有
,总有![]() ∥平面
∥平面![]() ;
;
(2)当![]() 的长度最小时,求二面角
的长度最小时,求二面角![]() 的平面角的余弦值。
的平面角的余弦值。
【答案】(1)见解析;(2)![]()
【解析】
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,作
,作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .通过证明四边形
.通过证明四边形![]() 为平行四边形,可得
为平行四边形,可得![]() ∥
∥![]() ,再根据直线与平面平行的判断定理可证.
,再根据直线与平面平行的判断定理可证.
(2)根据题意计算得![]()
![]()
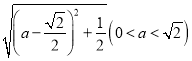 ,再配方可得
,再配方可得![]() 取最小值时
取最小值时![]() 分别为
分别为![]() 的中点,再取
的中点,再取![]() 为
为![]() , 连接
, 连接![]() ,
,![]() ,
,![]() ,
,
可得![]() 是二面角
是二面角![]() 的平面角,再计算可得.
的平面角,再计算可得.
(1)证明:如图,作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,
,
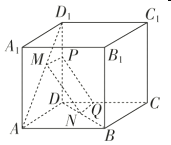
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
由题意得![]() ∥
∥![]() ,且
,且![]() ,则四边形
,则四边形![]() 为平行四边形.
为平行四边形.
∴![]() ∥
∥![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() ∥
∥![]() .
.
(2)由(1)知四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .
.
即![]() ,
,
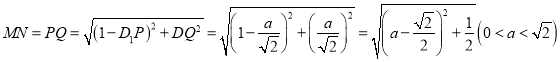
故当![]() 时,
时,![]() 的长度有最小值。
的长度有最小值。
分别取![]() ,
,![]() 的中点
的中点![]() 、
、![]() ,连接
,连接![]() ,
,![]() ,
,![]() 。
。
易知![]() ,
,![]() ,故
,故![]() 是二面角
是二面角![]() 的平面角
的平面角
在![]() 中,
中,![]() 。所以
。所以![]() .
.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
【题目】从某工厂的一个车间抽取某种产品![]() 件,产品尺寸(单位:
件,产品尺寸(单位:![]() )落在各个小组的频数分布如下表:
)落在各个小组的频数分布如下表:
数据分组 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)根据频数分布表,求该产品尺寸落在![]() 的概率;
的概率;
(2)求这![]() 件产品尺寸的样本平均数
件产品尺寸的样本平均数![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经过计算得
,经过计算得![]() ,利用该正态分布,求
,利用该正态分布,求![]() .
.
附:①若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ;②
;②![]() .
.