题目内容
设A是数集,满足a∈A时,必有
∈A,
(1)若2∈A,问:
①A中至少有几个元素?并把它列举出来?
②A中还可以有其它元素吗?
(2)若A中只能有一个元素且2∉A,实数a是否存在?
| 1 |
| 1-a |
(1)若2∈A,问:
①A中至少有几个元素?并把它列举出来?
②A中还可以有其它元素吗?
(2)若A中只能有一个元素且2∉A,实数a是否存在?
考点:元素与集合关系的判断
专题:集合
分析:(1)①根据题意,可得若2∈A,则在A中还有两个元素是:
=-1,
=
,据此解答即可;
②假设还有其他元素,利用满足a∈A时,必有
∈A,进一步
=1-
∈A,
=a∈A,得到A中可以有其他元素;
(2)假设存在,利用一直得到解答.
| 1 |
| 1-2 |
| 1 |
| 1+1 |
| 1 |
| 2 |
②假设还有其他元素,利用满足a∈A时,必有
| 1 |
| 1-a |
| 1 | ||
1-
|
| 1 |
| a |
| 1 | ||
1-(1-
|
(2)假设存在,利用一直得到解答.
解答:
解:(1)①根据题意,可得若2∈A,则在A中还有两个元素是:
=-1,
=
,所以A中至少有3个元素,分别是2,-1,
;
②假设还有其他元素,因为a∈A时,必有
∈A,所以
=1-
∈A,所以
=a∈A,得到A中可以有其他元素;
(2)若A中只能有一个元素且2∉A,实数a假设存在,则a=
=1-
无解,所以假设错误;所以若A中只能有一个元素且2∉A,实数a不存在.
| 1 |
| 1-2 |
| 1 |
| 1+1 |
| 1 |
| 2 |
| 1 |
| 2 |
②假设还有其他元素,因为a∈A时,必有
| 1 |
| 1-a |
| 1 | ||
1-
|
| 1 |
| a |
| 1 | ||
1-(1-
|
(2)若A中只能有一个元素且2∉A,实数a假设存在,则a=
| 1 |
| 1-a |
| 1 |
| a |
点评:本题考查了元素与集合的关系,主要根据集合元素的特征进行求解,对于存在型的问题,需要先假设存在有条件列出方程进行求解说明.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
设p:f(x)=x3-2x2-mx+1在(-∞,+∞)上单调递增;q:m>
,则p是q的( )
| 4 |
| 3 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、以上都不对 |
一个物体的运动方程为s=1-t+t2其中s的单位是米,t的单位是秒,那么物体在t=4时的瞬时速度是( )
| A、7米/秒 | B、6米/秒 |
| C、5米/秒 | D、8米/秒 |
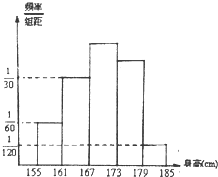 某校对高三年级男生的身体发育情况进行调查,共抽取60名男生的身高作为样本,其频率分布直方图如图所示,则身高在[167,179)之间的人数为( )
某校对高三年级男生的身体发育情况进行调查,共抽取60名男生的身高作为样本,其频率分布直方图如图所示,则身高在[167,179)之间的人数为( )