题目内容
若函数f（x）=ax-lnx在（1，+∞）上是增函数，则实数a的取值范围是（ ）
| A、（-∞，1） |
| B、（-∞，1] |
| C、（1，+∞） |
| D、[1，+∞） |
考点：利用导数研究函数的单调性
专题：计算题,导数的综合应用
分析：由题意求导f′（x）=a-
=
；化单调性为导数的正负问题，从而求解．
| 1 |
| x |
| ax-1 |
| x |
解答：
解：∵f（x）=ax-lnx，
∴f′（x）=a-
=
；
∵函数f（x）=ax-lnx在（1，+∞）上是增函数，
∴a-1≥0；
故a≥1；
故选D．
∴f′（x）=a-
| 1 |
| x |
| ax-1 |
| x |
∵函数f（x）=ax-lnx在（1，+∞）上是增函数，
∴a-1≥0；
故a≥1；
故选D．
点评：本题考查了导数的综合应用，属于中档题．
练习册系列答案
相关题目
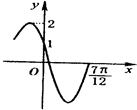
如图是函数f（x）=Asin（ωx+φ）（A＞0，0＜ω＜3，0＜φ＜π）的图象的一部分，则ωφ=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
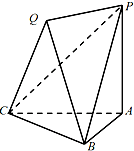在空间几何体PQ-ABC中，PA⊥平面ABC，平面QBC⊥平面ABC，AB=AC，QB=QC．