题目内容
若0<α<
<β<π,cos(β-
)=
,sin(α+β)=
.
(1)求sin2β;
(2)求cos(α+
);
(3)求cosβ.
| π |
| 2 |
| π |
| 4 |
| 5 |
| 13 |
| 4 |
| 5 |
(1)求sin2β;
(2)求cos(α+
| π |
| 4 |
(3)求cosβ.
考点:两角和与差的余弦函数,两角和与差的正弦函数
专题:三角函数的求值
分析:(1)利用sin2β=cos(
-2β)=cos(2β-
)由倍角公式求之;
(2)求出sin(β-
)=
,cos(α+β)=-
,利用cos(α+
)=cos[(α+β)-(β-
)]展开求之;
(3)cosβ=cos(β-
+
)展开求之.
| π |
| 2 |
| π |
| 2 |
(2)求出sin(β-
| π |
| 4 |
| 12 |
| 13 |
| 3 |
| 5 |
| π |
| 4 |
| π |
| 4 |
(3)cosβ=cos(β-
| π |
| 4 |
| π |
| 4 |
解答:
解:(1)sin2β=cos(
-2β)=cos(2β-
)=2cos2(β-
)-1=2×(
)2-1=-
;
(2)因为0<α<
<β<π,cos(β-
)=
,sin(α+β)=
.
所以sin(β-
)=
,cos(α+β)=-
,
cos(α+
)=cos[(α+β)-(β-
)]=cos(α+β)cos(β-
)+sin(α+β)sin(β-
)=-
×
+
×
=
;
(3)cosβ=cos(β-
+
)=cos(β-
)cos
-sin(β-
)sin
=
×
-
×
=-
.
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 5 |
| 13 |
| 119 |
| 169 |
(2)因为0<α<
| π |
| 2 |
| π |
| 4 |
| 5 |
| 13 |
| 4 |
| 5 |
所以sin(β-
| π |
| 4 |
| 12 |
| 13 |
| 3 |
| 5 |
cos(α+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 5 |
| 5 |
| 13 |
| 4 |
| 5 |
| 12 |
| 13 |
| 33 |
| 65 |
(3)cosβ=cos(β-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 5 |
| 13 |
| ||
| 2 |
| 12 |
| 13 |
| ||
| 2 |
7
| ||
| 26 |
点评:本题考查了三角函数中角的等价变换求三角函数值,关键是发现角的关系以及角的符号,求出三角函数值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=
的图象关于( )对称.
| 1 |
| x |
| A、x轴 | B、y轴 | C、原点 | D、y=1 |
表提供了某厂节能降低技术改造后产生甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
根据表提供的数据,用最小二乘法求出y关于x的线性回归方程
=0.7x+a,则实数a的值为( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
 |
| y |
| A、0.35 | B、0.3 |
| C、0.4 | D、0.5 |
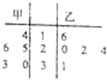 将甲、乙两名篮球运动员在篮球比赛中的得分制成茎叶图如图所示,若
将甲、乙两名篮球运动员在篮球比赛中的得分制成茎叶图如图所示,若. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,求时速在[60,70]的汽车大约有多少辆?
已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,求时速在[60,70]的汽车大约有多少辆?