题目内容
已知函数f（x）=2|x|，设g（x）=
，则函数g（x）的单调递减区间是（ ）
|
| A、[0，+∞） |
| B、[1，+∞） |
| C、（-∞，0] |
| D、（-∞，-1] |
考点：分段函数的应用
专题：函数的性质及应用
分析：化简函数g（x）的解析式，进而画出函数g（x）的图象，根据图象下降对应函数的单调递减区间，可得答案．
解答：
解：∵f（x）=2|x|，
∴g（x）=
=
，
其图象如下图所示：
，
由图可知：函数g（x）的单调递减区间是（-∞，-1]，
故选：D
∴g（x）=
|
|
其图象如下图所示：
，由图可知：函数g（x）的单调递减区间是（-∞，-1]，
故选：D
点评：本题考查的知识点是分段函数的应用，函数的图象，函数的单词性，其中画出函数g（x）的图象，是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
在f（x）=sinx、f（x）=2x、f（x）=2x+1、f（x）=log2x、f（x）=x2这五个函数中，四个正实数x1、x2、α、β满足x1≠x2、α≠β，则当|β-α|＞|x2-x1|时，使得不等式|f（β）-f（α）|＞|f（x2）-f（x1）|恒成立的函数的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
下列函数中，与函数f（x）=lnx有相同定义域的是（ ）
| A、f（x）=ex | ||||
B、f（x）=
| ||||
| C、f（x）=|x| | ||||
D、f（x）=
|
某人睡午觉醒来，发现表停了，他打开收音机想听电台整点报时，则他等待的时间不多于5分钟的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=2x+x3-2的零点所在区间是（ ）
| A、（-2，-1） |
| B、（-1，0） |
| C、（0，1） |
| D、（1，2） |
在斜二侧画法的规则下，下列结论正确的是（ ）
| A、角的水平放置的直观图不一定是角 |
| B、相等的角在直观图中仍然相等 |
| C、相等的线段在直观图中仍然相等 |
| D、若两条线段平行且相等，则在直观图中对应的两条线段仍然平行且相等 |
三棱锥的高为3，侧棱长均相等且为2
，底面是等边三角形，则这个三棱锥的体积为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
tan
=（ ）
| 2014π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
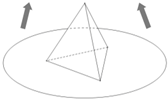某商场为促销要准备一些正三棱锥形状的装饰品，用半径为10cm的圆形包装纸包装．要求如下：正三棱锥的底面中心与包装纸的圆心重合，包装纸不能裁剪，沿底边向上翻折，其边缘恰好达到三棱锥的顶点，如图所示．设正三棱锥的底面边长为xcm，体积为Vcm3．在所有能用这种包装纸包装的正三棱锥装饰品中，V的最大值是多少？并求此时x的值．