题目内容
11. 已知正方体ABCD-A1B1C1D1,P是AD1中点,Q是BD中点,E是DD1中点.(1)求证:PQ∥平面D1DCC1;
已知正方体ABCD-A1B1C1D1,P是AD1中点,Q是BD中点,E是DD1中点.(1)求证:PQ∥平面D1DCC1;(2)求异面直线CE和DP所成角的余弦值.
分析 (1)连接AC,CD1,推导出PQ∥CD1,由此能证明PQ∥平面D1DCC1.
(2)取A1D1中点F,连接FP,FE,FC,推导出四边形FPDE是平行四边形,从而∠FEC或其补角中的锐角或直角为异面直线CE和DP所成角,由此能求出异面直线CE和DP所成角的余弦值.
解答 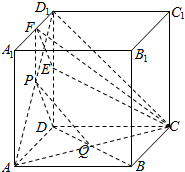 证明:(1)连接AC,CD1,
证明:(1)连接AC,CD1,
∵底面ABCD为正方形,Q是BD中点,
∴Q是AC中点,又P是AD1中点,∴PQ∥CD1,
∵CD1?平面D1DCC1,PQ?平面D1DCC1,
∴PQ∥平面D1DCC1.
解:(2)取A1D1中点F,连接FP,FE,FC,
设正方体棱长为a.
∴FP$\underline{\underline{∥}}$$\frac{1}{2}A{A_{1,}}又E是D{D_1}中点$,∴$DE\underline{\underline{∥}}\frac{1}{2}A{A_1}$,∴$FP\underline{\underline{∥}}DE$.
故四边形FPDE是平行四边形,∴FE∥DP
∴∠FEC或其补角中的锐角或直角为异面直线CE和DP所成角.
在$△EFC中,FE=\frac{{\sqrt{2}}}{2}a,EC=\frac{{\sqrt{5}}}{2}a,FC\frac{3}{2}a$.
$cos∠FEC=\frac{{F{E^2}+E{C^2}-F{C^2}}}{2FE•EC}=-\frac{{\sqrt{10}}}{10}$
∴异面直线CE和DP所成角的余弦值为$\frac{{\sqrt{10}}}{10}$.
点评 本题考查线面平行的证明,考查异面直线所成角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.椭圆以双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的焦点为顶点,以双曲线顶点为焦点,则椭圆的标准方程为( )
| A. | $\frac{y^2}{25}+\frac{x^2}{9}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{9}=1$ | C. | $\frac{y^2}{25}+\frac{x^2}{16}=1$ | D. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ |
16.已知经过点A(-2,0)和点B(1,3a)的直线l1与经过点P(0,-1)和点Q(a,-2a)的直线l2互相垂直,则实数a的值为( )
| A. | -1 | B. | 0 | C. | -1或0 | D. | 1或0 |
3.已知圆的半径为4,其内接三角形的三边长分别为a,b,c,若$abc=16\sqrt{2}$,则该三角形的面积为( )
| A. | $8\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
20.$\root{4}{{{{(-2)}^4}}}$的运算结果是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 不确定 |