题目内容
已知圆C过点M(0,3),N(1,4),且圆心C在直线x-y+4=0上.
(1)求圆C的方程;
(2)已知点P是抛物线y=x2上一点(异于原点),过点P作圆C的两条切线,交抛物线于A,B两点,若过C,P两点的直线l垂直于AB,求直线l的方程.
(1)求圆C的方程;
(2)已知点P是抛物线y=x2上一点(异于原点),过点P作圆C的两条切线,交抛物线于A,B两点,若过C,P两点的直线l垂直于AB,求直线l的方程.
考点:直线与圆锥曲线的综合问题,直线和圆的方程的应用
专题:圆锥曲线的定义、性质与方程
分析:(1)根据条件,结合两点间的距离公式即可求圆C的方程;
(2)设出点P的坐标,利用过点P作圆M的两条切线,交抛物线于A,B两点,设出点A,B的坐标,再设出过P的圆C的切线方程,利用交与抛物线两点,联立两个方程,利用根与系数之间的关系,得到两切线的斜率的式子,由已知的MP⊥AB,得到方程进而求解.
(2)设出点P的坐标,利用过点P作圆M的两条切线,交抛物线于A,B两点,设出点A,B的坐标,再设出过P的圆C的切线方程,利用交与抛物线两点,联立两个方程,利用根与系数之间的关系,得到两切线的斜率的式子,由已知的MP⊥AB,得到方程进而求解.
解答:
解:(1)∵圆心C在直线x-y+4=0,
∴设圆心C(a,a+4),
∵圆C过点M(0,3),N(1,4),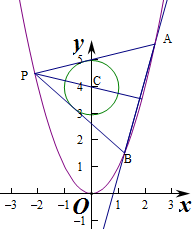
∴r=|CM|=|CN|,
即
=
,
即(a+1)2=(a-1)2,
解得a=0,即圆心C(0,4),半径R=|CM|=1,
则圆的方程为x2+(y-4)2=1.
(2)设点P(x0,x02),A(x1,x12),B(x2,x22),
由题意得:x0≠0,x1≠x2,
设过点P的圆M的切线方程为:y-x02=k(x-x0),
即y=kx-kx0+x02①
则
=1,
即(x02-1)k2+2x0(4-x02)k+(x02-4)2-1=0,
设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2应该为上述方程的两个根,
∴k1+k2=
,k1•k2=
;
代入①得:x2-kx+kx0-x02=0,则x1,x2应为此方程的两个根,
故x1=k1-x0,x2=k2-x0
∴kAB=x1+x2=k1+k2-2x0=
-2x0,kMP=
,
∵MP⊥AB,∴kAB•KMP=-1,
∴[
-2x0]•
=-1
∴解得x0=±
∴P(±
,
),直线l的方程为:y=±
x+4.
∴设圆心C(a,a+4),
∵圆C过点M(0,3),N(1,4),

∴r=|CM|=|CN|,
即
| a2+(a+4-3)2 |
| (a-1)2+a2 |
即(a+1)2=(a-1)2,
解得a=0,即圆心C(0,4),半径R=|CM|=1,
则圆的方程为x2+(y-4)2=1.
(2)设点P(x0,x02),A(x1,x12),B(x2,x22),
由题意得:x0≠0,x1≠x2,
设过点P的圆M的切线方程为:y-x02=k(x-x0),
即y=kx-kx0+x02①
则
| |kx0+4-x02| | ||
|
即(x02-1)k2+2x0(4-x02)k+(x02-4)2-1=0,
设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2应该为上述方程的两个根,
∴k1+k2=
| 2x0(x02-4) |
| x02-1 |
| (x02-4)2-1 |
| x02-1 |
代入①得:x2-kx+kx0-x02=0,则x1,x2应为此方程的两个根,
故x1=k1-x0,x2=k2-x0
∴kAB=x1+x2=k1+k2-2x0=
| 2x0(x02-4) |
| x02-1 |
| x02-4 |
| x0 |
∵MP⊥AB,∴kAB•KMP=-1,
∴[
| 2x0(x02-4) |
| x02-1 |
| x02-4 |
| x0 |
∴解得x0=±
|
∴P(±
|
| 23 |
| 5 |
3
| ||
| 115 |
点评:本题主要考查圆的标准方程,还考查了相应的曲线性质即设出直线方程,利用根与系数的思想整体代换,综合性较强,运算量较大,有一点的难度.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
若实数x,y满足不等式组
则当
≤2a恒成立时,实数a的取值范围是( )
|
| y-x |
| x+1 |
| A、[2,+∞) | ||
B、[-
| ||
C、[-
| ||
D、[-
|
 已知函数f(x)=2sin(
已知函数f(x)=2sin(