题目内容
在△ABC中,点O满足
=2
,过O点的直线分别交射线AB,AC于不同的两点M,N,若
=m
,
=n
,则mn的最大值是 .
| BO |
| OC |
| AB |
| AM |
| AC |
| AN |
考点:基本不等式
专题:不等式的解法及应用,平面向量及应用
分析:如图所示,
=
+
,
=
+
,利用
=2
,可得
=
m
+
n
.由于O、M、N三点共线,利用共线定理可得
m+
=1,再利用基本不等式即可得出.
| BO |
| BA |
| AO |
| OC |
| OA |
| AC |
| BO |
| OC |
| AO |
| 1 |
| 3 |
| AM |
| 2 |
| 3 |
| AN |
| 1 |
| 3 |
| 2n |
| 3 |
解答:
解:如图所示,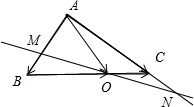
=
+
,
=
+
,
∵
=2
,
∴-
+
=2(
-
),
化为
=
m
+
n
,
∵O、M、N三点共线,
∴
m+
=1,化为m+2n=3.
只考虑m,n>0的情况,3=m+2n≥2
,化为mn≤
,当且仅当m=2n=
时取等号.
故答案为:
.

| BO |
| BA |
| AO |
| OC |
| OA |
| AC |
∵
| BO |
| OC |
∴-
| AB |
| AO |
| AC |
| AO |
化为
| AO |
| 1 |
| 3 |
| AM |
| 2 |
| 3 |
| AN |
∵O、M、N三点共线,
∴
| 1 |
| 3 |
| 2n |
| 3 |
只考虑m,n>0的情况,3=m+2n≥2
| 2mn |
| 9 |
| 8 |
| 3 |
| 2 |
故答案为:
| 9 |
| 8 |
点评:本题考查了向量的三角形法则、向量共线定理、基本不等式的性质等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
设全集U=R,集合A={x|2 x2-2x<1},B={x|x>1},则集合A∩∁UB等于( )
| A、{x|0<x<1} |
| B、{x|0<x≤1} |
| C、{x|0<x<2} |
| D、{x|x≤1} |