题目内容
曲线y=2sinx(0≤x≤π)与直线y=1围成的封闭图形的面积为______.
令2sinx=1(0≤x≤π),即sinx=
,可得x=
或
.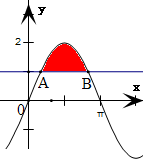
∴曲线y=2sinx(0≤x≤π)与直线y=1交于点A(
,1)和B(
,1),
因此,围成的封闭图形的面积为
S=
(2sinx-1)dx=(-2cosx-x)
=(-2cos
-
)-(-2cos
-
)=2
-
.
故答案为:2
-
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |

∴曲线y=2sinx(0≤x≤π)与直线y=1交于点A(
| π |
| 6 |
| 5π |
| 6 |
因此,围成的封闭图形的面积为
S=
| ∫ |
|
| | |
|
=(-2cos
| 5π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| 2π |
| 3 |
故答案为:2
| 3 |
| 2π |
| 3 |

练习册系列答案
相关题目

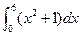 =
=