题目内容
14.设a>0,b>0,e是自然对数的底数)以下命题正确的为( )| A. | 若ea+2a=eb+3b,则a>b | B. | 若ea+2a=eb+3b,则a<b | ||
| C. | 若ea-2a=eb-3b,则a>b | D. | 若ea-2a=eb-3b,则a<b |
分析 利用指数函数的单调性、作差法即可判断出结论.
解答 解:对于A.ea+2a=eb+3b,则ea-eb=3b-2a,若a>b,则ea-eb>0,而3b-2a>0不一定成立.
对于B.ea+2a=eb+3b,则ea-eb=3b-2a,若a<b,则ea-eb<0,而3b>3a>2a,因此一定成立.
同理可得:C,D不正确.
故选:B.
点评 本题考查了指数函数的单调性、作差法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
4.若数列{an}满足(2n+3)an+1-(2n+5)an=(2n+3)(2n+5)lg(1+$\frac{1}{n}$),且a1=5,则数列{$\frac{{a}_{n}}{2n+3}$}的第2016项为( )
| A. | lg2017 | B. | lg2016 | C. | 1+lg2016 | D. | 1+lg2017 |
5.一个几何体的三视图,则它的体积为( )
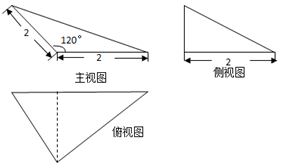

| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
2.直线y=-x+b与曲线$y=\sqrt{4-{x^2}}$有且只有两个公共点,则b的取值范围是( )
| A. | 2<b<2$\sqrt{2}$ | B. | 2≤b<2$\sqrt{2}$ | C. | 2≤b≤2$\sqrt{2}$ | D. | 2<b≤2$\sqrt{2}$ |
3.两个变量y和x进行回归分析,得到一组样本数据(x1,y1),(x2,y2),…,(xn,yn),则下列说法中不正确的是( )
| A. | 由样本数据得到的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$必过样本点的中心($\overline{x}$,$\overline{y}$) | |
| B. | 残差平方和越小的模型,拟合的效果越好 | |
| C. | 用相关指数R2来刻画回归效果,R2越小说明拟合效果越好 | |
| D. | 若变量y和x之间的相关系数为r=-0.9462,则变量y和x之间具有线性相关关系 |
4.在△ABC中,已知A=30°,a=8,则△ABC的外接圆直径是( )
| A. | 10 | B. | 12 | C. | 14 | D. | 16 |